Гравитационные волны могут захватывать частицы аналогично лазерным лучам в оптических ловушках, выяснили польские физики-теоретики. Они показали, что на малых масштабах гравитационная волна, испускаемая при слиянии массивных объектов, аналогична лучу Бесселя, и решили уравнения движения частицы, которая движется на фоне такого луча. Статья опубликована в Physical Review Letters, препринт работы выложен на сайте arXiv.org.

В этом году Нобелевскую премию по физике присудили за разработку оптического пинцета — прибора, который позволяет очень аккуратно перемещать маленькие объекты, практически не разрушая их структуру. Оптический пинцет работает за счет градиентных сил — эти силы возникают в лазерном пучке, который несет ненулевой угловой момент, и «прижимают» частицы к его центру. Подробнее про градиентные силы можно прочитать в нашем материале «Скальпель и пинцет». В свое время открытие градиентных сил и разработка оптического пинцета позволила ученым подробно исследовать бактерии и другие микрометровые живые организмы, а также охладить нейтральные атомы до сверхнизких температур и впервые получить на практике конденсат Бозе — Эйнштейна.

С другой стороны, электромагнитные силы отдаленно напоминают силы гравитационного притяжения — обе силы переносятся безмассовыми частицами и имеют неограниченно большой радиус действия, а закон Ньютона, который приближенно описывает гравитацию при малой кривизне пространства-времени, совпадает с законом Кулона. Более того, в Общей теории относительности существуют гравитационные волны — колебания метрики, которые распространяются со скоростью света и могут переносить угловой момент. Поэтому можно ожидать, что некоторые электромагнитные явления — например, градиентная сила — будут иметь аналоги в гравитации. Тем не менее, нужно помнить, что в действительности Общая теория относительности и электродинамика — это две принципиально разные теории; например, электромагнитные волны — векторные, а гравитационные — тензорные. Поэтому все совпадения скорее случайны, чем закономерны.

Физики-теоретики Иво Бялыницкий-Бирула (Iwo Bialynicki-Birula) и Шимон Хажиньский (Szymon Charzyński) показали, что гравитационные волны в Общей теории относительности действительно могут связывать частицы подобно электромагнитным волнам в оптических ловушках. Для этого ученые рассмотрели движение частиц на фоне луча Бесселя — аксиально-симметричных колебаний метрики, амплитуда которых описывается функцией Бесселя. В реальности такие лучи существовать не могут, поскольку они создают бесконечно большой поток энергии, однако их можно использовать в качестве удобного приближения для гравитационных волн, испускаемых при слиянии двух массивных объектов — например, нейтронных звезд или черных дыр. В самом деле, ученые показали, что поблизости от объекта обе картины колебаний практически совпадают. В качестве примера они рассчитали излучение от системы двух черных дыр массой порядка 30 масс Солнца, которые вращаются вокруг общего центра с частотой 0,5 герц — такая частота отвечает моменту, когда до слияния черных дыр осталось около четырех дней, — а затем показали, что в радиусе 10 длин волн излучение системы эквивалентно лучу Бесселя с частотой около одного герца.

Продольная компонента углового момента колебаний метрики на расстоянии 10 длин волн от источника. Сплошной линией отмечены реальные гравитационные волны, пунктирной линией — усредненное значение, прерывистой линией — распределение для луча Бесселя/I. Bialynicki-Birula & S. Charzyński / Physical Review Letters

После этого физики выписали уравнения движения частиц, которые движутся на фоне луча Бесселя, отвечающего гравитонам с угловым моментом M = 2ℏ. Ученые связывают колебания метрики с гравитонами, чтобы подчеркнуть сходство с электродинамикой, однако считают, что гравитонов достаточно много, чтобы для описания движения частиц можно было использовать классическую теорию (ОТО). Чтобы найти траектории частиц, исследователи сделали замену переменных и перешли в систему отсчета, которая равномерно вращается вокруг оси гравитационной волны, и проинтегрировали в ней найденные уравнения движения. В результате оказалось, что из-за эффекта Кориолиса частицы захватываются волной и начинают двигаться вдоль ее оси, причем этот эффект сохраняется при возвращении в исходную систему отсчета. Интересно, что захват частиц происходит только в том случае, если гравитационная волна не очень сильная. Впрочем, на практике это означает, что радиус орбиты гравитирующих тел и расстояние до частицы должны быть одновременно равны радиусу Шварцшильда. Как правило, на практике оба расстояния гораздо больше.

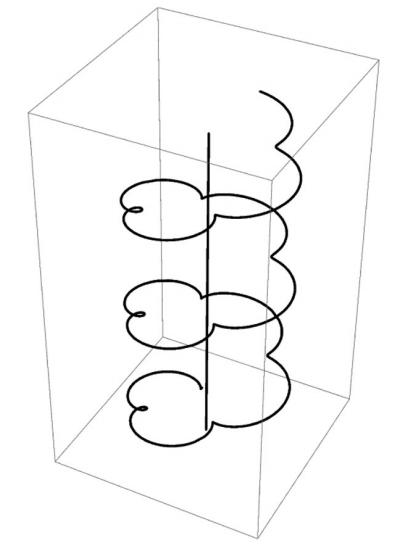Траектория частицы, которая движется на фоне луча Бесселя/I. Bialynicki-Birula & S. Charzyński / Physical Review Letters

Авторы статьи отмечают, что они рассмотрели самый простой случай, который позволяет только качественно увидеть захват частиц гравитационными волнами. Тем не менее, ученые считают, что те же самые эффекты должны наблюдаться в произвольных гравитационных волнах, которые имеют ненулевой угловой момент. Более того, авторы считают, что эти эффекты могут повлиять на формирование галактических джетов.

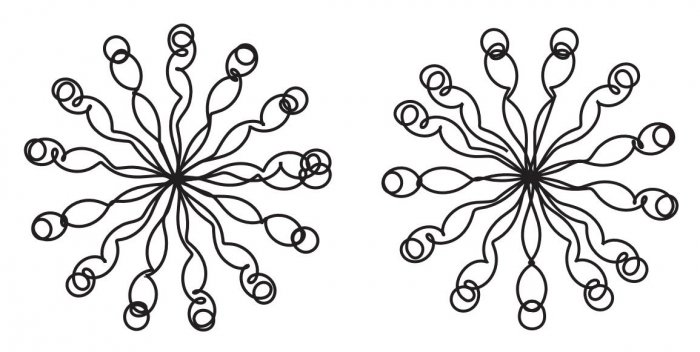Сравнение проекций траекторий частиц на плоскость, перпендикулярную направлению волны: случай электромагнитной (слева) и гравитационной волны (справа)/I. Bialynicki-Birula & S. Charzyński / Physical Review Letters

Интересно, что за время, которое прошло между принятием и публикацией статьи, группа ученых под руководством Питера Хорвати (Peter Horvathy) опубликовала работу, в которой также проводились аналогии между гравитационными волнами и оптической ловушкой. Тем не менее, в этой работе ученые рассматривали гравитационные волны с круговой поляризацией, которые могут возникать в моделях инфляции, а не лучи Бесселя.

Автор: Дмитрий Трунин