В зависимости от поведения во внешнем магнитном поле сверхпроводники принято делить на 1-й и 2-й род. Открытие в 2001 году «необычной» сверхпроводимости в дибориде магния вызвало дискуссию: к какому роду следует отнести данный сверхпроводник?

Некоторые ученые полагают, что диборид магния не укладывается в общепринятую классификацию, а образует совершенно новую категорию — сверхпроводников 1,5-го рода, вобравших в себя часть свойств от сверхпроводников 1-го рода и часть от 2-го. Другие ученые не согласны с такой интерпретацией, утверждая, что «необычные» сверхпроводники вполне укладываются в рамки существующего деления на 1-й и 2-й род. Этим летом история с полуторной сверхпроводимостью получила свое продолжение. Данная новость — логическое продолжение двух предыдущих. Вкратце напомним их содержание.

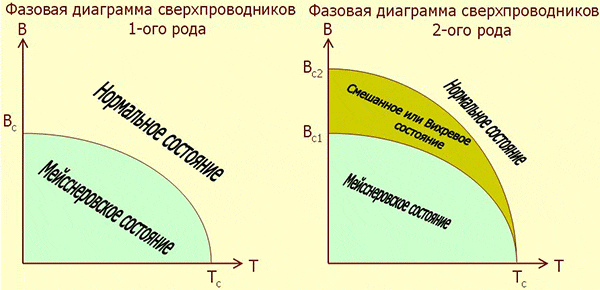Рис. 1. Фазовая диаграмма состояния сверхпроводников 1-го и 2-го рода, показывающая, как меняются состояния сверхпроводника при изменении температуры и индукции внешнего магнитного поля. В мейсснеровском состоянии силовые линии магнитного поля не могут проникнуть в вещество. Смешанное или вихревое состояние означает сосуществование сверхпроводимости и нормальных несверхпроводящих тонких ниток, вытянутых вдоль силовых линий магнитного поля. Такие нитки называют вихрями Абрикосова, или квантовыми вихрями (см. подробности в тексте). Рисунок Юрия Ерина.

Основные характеристики сверхпроводящего состояния и способы его математического описания:

1. Критическая температура (T_c). Сверхпроводимость — состояние вещества, при котором оно обладает нулевым электрическим сопротивлением и одновременно с этим не пропускает через себя внешнее магнитное поле, — возникает, когда температура вещества становится ниже определенного значения T_c. Критическая температура — одна из самых важных характеристик любого сверхпроводника.
2. Идеальный диамагнетизм (также: эффект Мейсснера–Оксенфельда, мейсснеровское состояние, мейсснеровская фаза) — выталкивание внешнего магнитного поля при переходе в сверхпроводящее состояние (сверхпроводник не дает силовым линиям магнитного поля себя пронизывать). Идеальный диамагнетизм возникает за счет того, что внешнее магнитное поле генерирует в очень тонком приповерхностном слое вещества сверхпроводящие (мейсснеровские) токи, которые создают магнитное поле противоположной направленности и такой же силы.
3. Лондоновская глубина проникновения (λ) — глубина слоя, которую оккупировали мейсснеровские токи.
4. Длина когерентности (ξ). В середине 50-х годов прошлого века американские физики Нейл Купер, Джон Бардин и Джон Шриффер показали, что сверхпроводимость обусловлена корреляциями между электронами проводимости (электроны объединяются в так называемые куперовские пары). За счет этого все электроны проводимости ведут себя как единое целое, а потому могут бездиссипативно (без потерь энергии) двигаться через кристаллическую решетку вещества. В этой теории сверхпроводимости (теории БКШ) масштаб корреляций электронов, или (грубо говоря) размер куперовской пары, называется длиной когерентности.
5. Энергетическая щель (Δ). Не вдаваясь в подробности, просто заметим, что величина энергии связи двух электронов в куперовской паре равна 2Δ.

Теория и эксперимент показывают, что лондоновская глубина проникновения (λ), длина когерентности (ξ) и энергетическая щель (Δ) не являются константами, а зависят от температуры и обладают сугубо индивидуальными для заданного материала величинами. Величины λ и ξ имеют минимальное значение при T = 0 и монотонно возрастают с увеличением температуры, стремясь к бесконечности при T = T_c (это объясняется тем, что выше критической температуры никаких куперовских пар нет, а магнитное поле беспрепятственно пронизывает вещество). Энергетическая щель (Δ), наоборот, имеет максимум при T = 0 и становится равной нулю при T = T_c (что можно трактовать как отсутствие каких-либо корреляций между электронами).

Теория БКШ дает исчерпывающее описание сверхпроводящих свойств материала во всём температурном интервале от 0 до T_c, но является сложной с математической точки зрения. Поэтому часто физики прибегают к другому, относительно более простому способу анализа сверхпроводящего состояния — теории Гинзбурга–Ландау, которая прекрасно описывает, качественно и количественно, поведение сверхпроводника, но работает только в ограниченном интервале вблизи критической температуры.

Теория Гинзбурга–Ландау основывается на теории фазовых переходов 2-го рода (к ним относится и переход вещества в сверхпроводящее состояние). В этой теории, наряду с критической температурой, длиной когерентности и лондоновской глубиной проникновения, вводится еще одна характеристика,  — параметр порядка (комплексная величина). С точностью до некоторого коэффициента пропорциональности можно считать, что модуль параметра порядка — это энергетическая щель в теории БКШ. Параметр порядка равен нулю при T = T_c и выше и принимает максимальное значение, когда температура достигла абсолютного нуля. Отметим, что есть и иная трактовка физического смысла параметра порядка: квадрат его модуля определяет концентрацию куперовских пар.

Параметр порядка играет ключевую роль в теории Гинзбурга–Ландау. Через него выражается энергия (с точки зрения термодинамики корректнее говорить свободная энергия) сверхпроводника.

Сверхпроводимость 1-го и 2-го рода

Несмотря на то что теория Гинзбурга–Ландау является феноменологической, то есть она не объясняет причины возникновения явления, которое она описывает, с ее помощью был получен ряд важных результатов. Применив эту теорию, ее авторы вычислили разность энергий (так называемую поверхностную энергию), возникающую на границе сверхпроводника и нормального металла в присутствии внешнего магнитного поля. Оказалось, что результат зависит от безразмерной величины, называемой параметром Гинзбурга–Ландау (κ): κ = λ/ξ (отношение лондоновской глубины проникновения к длине когерентности). Из расчетов следовало, что при κ < 1/√2 поверхностная энергия оказывается положительной. Для сверхпроводника цилиндрической формы, ось которого параллельна силовым линиям магнитного поля, данный результат означал, что переход в нормальное состояние происходит моментально, как только индукция магнитного поля превышает некоторое критическое значение Bc для данной температуры (рис. 1). В принципе, ничего нового Гинзбург и Ландау не получили, они лишь теоретически подтвердили хорошо известный уже на тот момент экспериментальный факт поведения сверхпроводников. Однако дальше оказалось интереснее.

Советский физик Николай Заварицкий, исследуя тонкие сверхпроводящие пленки, обнаружил, что их поведение в магнитном поле не согласуется с предсказаниями теории Гинзбурга–Ландау. Чтобы понять причину расхождения, Алексей Абрикосов, основываясь на теории Гинзбурга–Ландау, решил рассмотреть случай, когда поверхностная энергия является отрицательной, — иными словами, попытаться понять картину поведения сверхпроводника в магнитном поле с κ > 1/√2.

И вот здесь обнаружилось удивительное. Из расчетов следовало, что пока индукция магнитного поля не превосходит некоторого предела B_c1 (нижнего критического поля) при фиксированной температуре, сверхпроводник находится в мейсснеровском состоянии. После того как индукция магнитного поля стала больше B_c1, сверхпроводник начинают пронизывать своеобразные нити микронных размеров, вытянутые вдоль силовых линий внешнего поля. Чем больше индукция поля, тем больше ниток будет в сверхпроводнике. Абрикосов установил, что эти образования представляют собой вихри (теперь они называются абрикосовскими), ядра которых являются несверхпроводящими, нормальными, с размером порядка длины когерентности ξ, а вокруг них протекают циркулирующие сверхпроводящие токи, которые экранируют нормальную область вихря (ширина области экранировки равна лондоновской глубине проникновения λ). Кроме того, в ходе вычислений обнаружилось, что вихри несут в себе как бы одну силовую линию внешнего магнитного поля, или квант магнитного потока, флюксоид Φ₀ = h/2e = 2,07·10^–15 Тл·м². Вихри формируют в сверхпроводнике треугольную решетку, образуя смешанное (оно же вихревое) состояние (рис. 1).

Если при заданной температуре продолжить усиливать магнитное поле, то при некотором значении Bc2 (верхнее критическое поле) вихрей станет настолько много, что их ядра начнут перекрываться, и они заполнят весь объем сверхпроводника, переводя его в нормальное состояние (рис. 1).

Сверхпроводимость 1,5-го рода и двухщелевые сверхпроводники

В 2001 году в дибориде магния MgB₂ была открыта сверхпроводимость с неожиданно высокой (для такого простого химического соединения) критической температурой 39 К. Применяя различные экспериментальные техники, ученые установили, что большое значение Tc достигается за счет наличия в MgB₂ не одной энергетической щели, а двух. Проще говоря, в сверхпроводящем дибориде магния присутствует как бы два сорта куперовских пар. Их взаимодействие и обеспечивает высокую T_c. Важно отметить, что у каждого сорта электронных пар есть свой размер, или своя длина когерентности. При этом диборид магния имеет лишь одну величину лондоновской глубины проникновения.

Открытие сверхпроводящего состояния в MgB₂ стимулировало огромный рост числа публикаций, посвященных теоретическому и экспериментальному исследованию сверхпроводимости с двумя щелями. Среди всего разнообразия задач, связанных с данной тематикой, особенно актуальным и спорным оказался вопрос о поведении таких сверхпроводников в магнитном поле.

Всё началось со статьи Semi-Meissner state and neither type-I nor type-II superconductivity in multicomponent superconductors Егора Бабаева и Мартина Спейта в журнале Physical Review B. Авторы работы задались вопросом: как будет вести себя двухщелевой сверхпроводник в магнитном поле, если предположить, что один сорт куперовских пар имеет параметр Гинзбурга–Ландау меньше 1/√2, то есть как бы образует сверхпроводник 1-го рода, а для второго сорта этот параметр больше 1/√2 (сверхпроводник 2-го рода)? Используя теорию Гинзбурга–Ландау, обобщенную на случай двух параметров порядка (по сути, на сверхпроводимость с двумя щелями), ученые предсказали существование в таком сверхпроводнике некоего полумейсснеровского состояния, характеризующегося, помимо других особенностей, образованием не треугольной вихревой решетки, как в сверхпроводниках 2-го рода, а неких скоплений (кластеров) вихревых молекул.

Формально, в сверхпроводниках 1-го рода тоже есть вихри. Только они там не являются стабильными образованиями. При первом появлении они начинают притягиваться друг другу, причем чем ближе они расположены, тем сильнее притяжение. Зависимость энергии взаимодействия двух вихрей от расстояния между ними представлена на рис. 2 (слева). Из графика видно, что энергия взаимодействия вихрей минимальна, когда расстояние между вихрями равно нулю. Из-за стремления вихрей уменьшить энергию своего взаимодействия они сливаются между собой и образуют нормальные области в сверхпроводнике. Этот процесс возникновения несверхпроводящих участков происходит чрезвычайно быстро, так что можно говорить о моментальном переходе из мейсснеровской фазы в нормальную.

В сверхпроводнике 2-го рода взаимодействие вихрей носит только отталкивающий характер: чем ближе вихри расположены друг к другу, тем сильнее они отталкиваются (рис. 2, справа). Минимум энергии наблюдается, когда вихри удалены друг от друга на бесконечно большое расстояние. Однако, поскольку сверхпроводник имеет конечные размеры, а вихрей может быть больше, чем два, взаимное отталкивание приводит к образованию стабильной структуры — треугольной вихревой решетки.

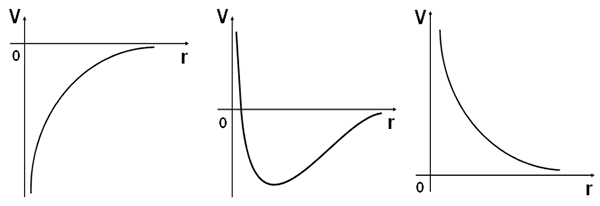Рис. 2. Зависимость энергии взаимодействия V двух вихрей от расстояния r между ними в сверхпроводнике 1-го рода (слева), 1,5-го рода (центр) и 2-го рода (справа). Положительные значения V соответствуют отталкиванию между вихрями, отрицательные — притяжению. Благодаря наличию минимума в точке r, где значение не равно нулю или бесконечности, может возникнуть сверхпроводимость 1,5-го рода (см. подробности в тексте). Рисунок Юрия Ерина.

В сверхпроводниках с двумя щелями, как выяснили Бабаев и Спейт, взаимодействие вихрей качественно совпадает с межмолекулярным взаимодействием: отталкивание на коротких расстояниях сменяется притяжением на далеких расстояниях (рис. 2, центр). Существование минимума энергии в отличной от нуля и бесконечности точке на оси r выражается в стремлении вихрей создавать неоднородные вихревые структуры, группироваться в некие кластеры или вихревые молекулы, когда вокруг определенного вихря на расстоянии, соответствующем этому самому минимуму, энергетически выгодно располагаться остальным вихрям. В итоге реализуется не мейсснеровское состояние (потому что вихри не «слиплись», как в сверхпроводнике 1-го рода), но в то же время и не смешанное (поскольку нет треугольной решетки, как в сверхпроводнике 2-го рода). Поэтому авторы статьи назвали такую фазу сверхпроводника полумейсснеровской.

Через четыре года после статьи Бабаева и Спейта группа физиков, возглавляемая Виктором Мощалковым, опубликовала в журнале Physical Review Letters статью об обнаружении неоднородной вихревой решетки в сверхпроводящем (двухщелевом) монокристалле диборида магния, предсказанной Бабаевым и Спейтом. Только теперь, с легкой руки авторов открытия, фаза MgB2 с неоднородной вихревой решеткой вместо полумейсснеровского состояния стала называться сверхпроводимостью 1,5-го рода. Тем самым подчеркивалось, что наблюдаемое неравномерное распределение вихрей находится как бы посередине между фазами сверхпроводимости 1-го и 2-го рода.

Надо сказать, что реакция на эту работу со стороны специалистов последовала весьма неоднозначная. Прежде всего, смущали чрезвычайно малые значения индукции магнитного поля, в которой наблюдалась сверхпроводимость 1,5-го рода, — от 0,0001 до 0,0005 Тл при температуре около 4 К. Недоумение вызывал тот факт, что, во-первых, экспериментальные данные указывают на то, что вплоть до 0,003 Тл в дибориде магния наблюдается исключительно мейсснеровская фаза, то есть никаких вихрей быть не должно. Во-вторых, ранее уже проводились исследования вихревых структур в MgB₂, и ученые действительно регистрировали неравномерное распределения вихрей. Однако идентифицировать его как сверхпроводимость 1,5-го рода никому не приходило в голову. Нерегулярную вихревую решетку в слабых полях исследователи связывали исключительно с явлением пиннинга — неизбежным присутствием в монокристалле дефектов и «слабых» мест, в которые проникает в виде вихрей даже очень слабое магнитное поле.

Этим летом дискуссия о существовании сверхпроводимости 1,5-го рода продолжилась, вернувшись в теоретическую плоскость. В Архиве электронных препринтов и в журналах Американского физического общества появилось несколько статей, в которых приводятся доказательства как существования полуторной сверхпроводимости в двухщелевых сверхпроводниках, так и ее отсутствия. Начнем с аргументов, указывающих на существование сверхпроводимости 1,5-го рода.

Аргументы в пользу существования сверхпроводимости 1,5-го рода

В первую очередь здесь стоит отметить статью Giant vortices, vortex rings and reentrant behavior in type-1.5 superconductors уже известной группы Мощалкова. Применяя теорию Гинзбурга–Ландау для двухщелевых сверхпроводников, авторы рассчитали возможные зависимости энергии взаимодействия двух вихрей от разделяющей их дистанции в таком сверхпроводнике (рис. 3а). В отличие от пионерской работы Бабаева и Спейта, ученые описали более реалистичную ситуацию в двухщелевом сверхпроводнике, считая, что два сорта куперовских пар взаимодействуют между собой. На рис. 3а приведена эволюция зависимости «энергия–расстояние» по мере увеличения силы взаимодействия двух сортов куперовских пар. График i соответствует слабому взаимодействию, график iv — сильному. Несмотря на то что зависимость i своим поведением напоминает зависимость энергии вихревого взаимодействия в сверхпроводнике 1-го рода, а зависимость iv похожа на аналогичную характеристику в сверхпроводнике 2-го рода, все зависимости обладают существенным отличием: у них есть минимум энергии взаимодействия двух вихрей, возникающий на отличном от нуля (случай сверхпроводника 1-го рода) или бесконечности (случай сверхпроводника 2-го рода) расстоянии.

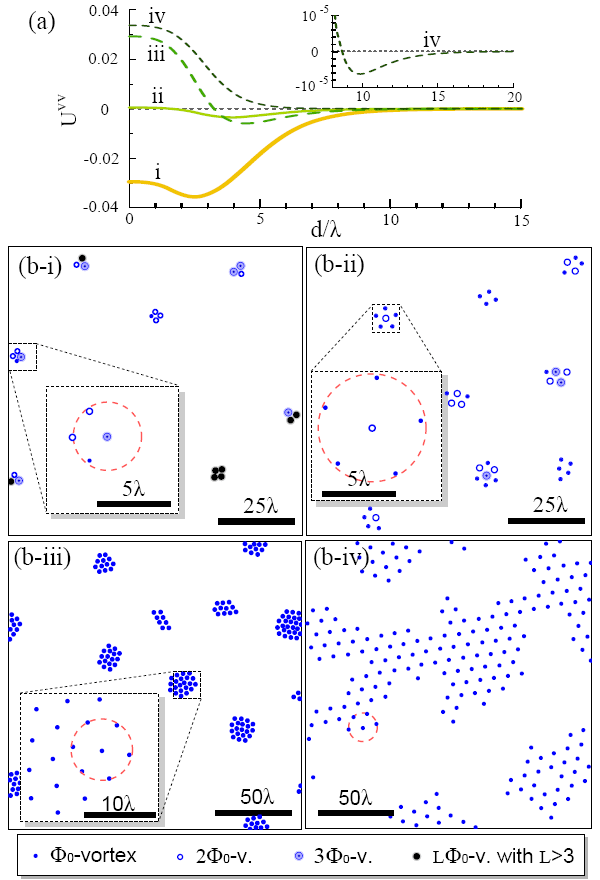Рис. 3. (а) Различные виды зависимостей энергии вихревого взаимодействия в сверхпроводнике 1,5-го рода (двухщелевом сверхпроводнике). На вставке представлено увеличенное изображение кривой iv. (b) Распределение вихрей, вытекающее из зависимостей i, ii, iii и iv. Возникающие вихри могут содержать более одного флюксоида Φ0. Выражение LΦ0 означает, что вихрь содержит L квантов магнитного потока. Красная пунктирная линия определяет наиболее выгодное с энергетической точки зрения расстояние между вихрями (соответствует минимуму на средней кривой на рис. 2). Масштаб измеряется в единицах лондоновской глубины проникновения для двухщелевого сверхпроводника. Изображения из статьи arXiv:1007.1849.

В качестве еще одного аргумента «за» заметим, что подобный ход зависимостей «энергия–расстояние» с учетом взаимодействия между разными сортами куперовских пар независимо был получен также в работе Бабаева, Спейта и Кальстрёма, опубликованной в журнале Physical Review Letters.

Исходя из рассчитанных зависимостей, с помощью метода молекулярной динамики исследователи промоделировали поведение 200 вихрей в квадратной сверхпроводящей пленке размером 200λ × 200λ. Видно (рис. 3b), что вихревая решетка имеет очевидную неоднородность.

Из вычислений Мощалкова и его коллег также следовало, что для двухщелевых сверхпроводников при включении внешнего магнитного поля сразу возникает состояние с неоднородным распределением вихрей, которое затем, при увеличении индукции поля (фиксированная температура) или увеличении температуры (фиксированная индукция магнитного поля), может смениться мейсснеровским состоянием либо знакомой уже треугольной вихревой решеткой.

Интересно, что для некоторого набора параметров сверхпроводника с двумя щелями его фазовая диаграмма становится экзотической. Например, при заданном магнитном поле и повышающейся температуре сверхпроводник испытывает переходы: состояние с неоднородной вихревой решеткой → состояние с треугольной вихревой решеткой → состояние с неоднородной вихревой решеткой → мейсснеровское состояние.

То, что магнитное поле в двухщелевые сверхпроводники сразу проникает в виде неравномерно расположенных вихрей, подтверждается в статье Vortex States and Phase Diagram of Multi-component Superconductors with Competing Repulsive and Attractive Vortex Interactions японских физиков. Идеология расчетов практически та же, что и в работе группы Мощалкова. Из теории Гинзбурга–Ландау для двухщелевых сверхпроводников вычисляется энергия взаимодействия двух вихрей, а затем проводится моделирование упорядочения большого количества (а именно, 400) вихрей в квадратной сверхпроводящей пленке для разных значений магнитного поля при заданной температуре.

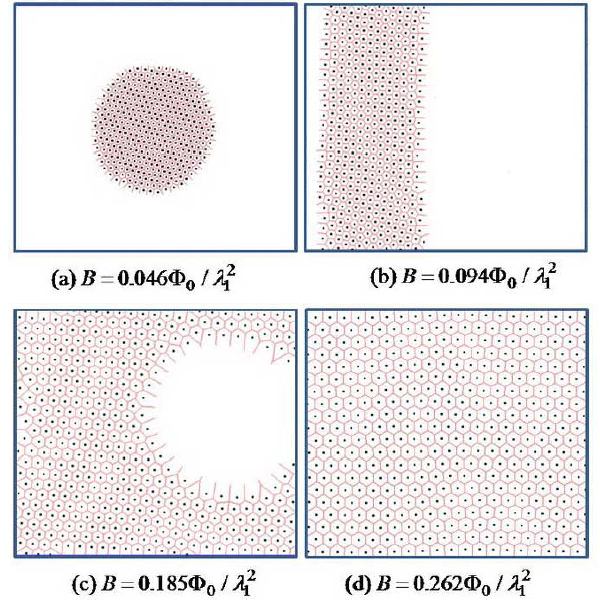Рис. 4. Конфигурации вихревых решеток в двухщелевой сверхпроводящей пленке в форме квадрата при различных значениях индукции магнитного поля, измеряемого в единицах Φ0 (квант магнитного потока) и λ1 (лондоновская глубина проникновения для первого сорта куперовских пар). (а) вихревой кластер (вихревая молекула), (b) вихревая полоса, © вихревая решетка с пустотой, (d) треугольная вихревая решетка. Черные точки соответствуют вихрям. Сторона пленки равна: (a) 100λ₁, (b) 70 λ₁, © 50λ₁, (d) 42λ₁. Изображение из статьи arXiv:1007.1940.

Вихревые структуры, возникающие в процессе роста индукции внешнего поля при заданной температуре, продемонстрированы на рис. 4. Увеличение магнитного поля сопровождается трансформацией от кластерной вихревой решетки до хорошо известной треугольной (рис. 4d), причем помимо полос, которые наблюдала в своем эксперименте команда Мощалкова, авторы статьи предсказывают еще и появление вихревых пустот (рис. 4с) — сверхпроводящих областей круглой формы с отсутствием вихрей.

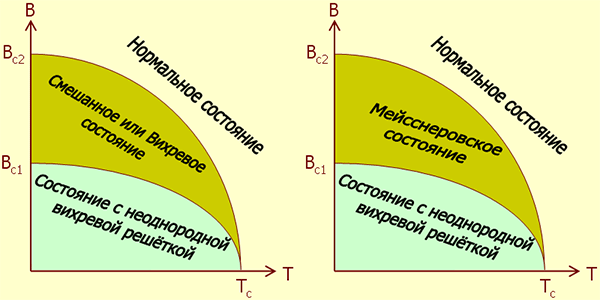Рис. 5. Вероятные фазовые диаграммы сверхпроводников 1,5-го рода. Различия в поведении определяются параметрами двухщелевого сверхпроводника. Рисунок Юрия Ерина.

Таким образом, суммируя описанные выше факты, можно построить вероятные (на качественном уровне) фазовые диаграммы двухщелевых сверхпроводников (рис. 5), у которых параметры Гинзбурга–Ландау для каждой из двух разновидностей куперовских пар соответственно меньше и больше 1/√2. Подчеркнем еще раз, что при постепенном увеличении от нуля индукции магнитного поля фазовая диаграмма сверхпроводника с двумя щелями «стартует» не с мейсснеровской фазы, как это имело место в сверхпроводнике 1-го или 2-го рода, а сразу с неоднородного вихревого состояния. Аргументы против существования сверхпроводимости 1,5-го рода

Как уже было сказано, количественный критерий деления сверхпроводников на 1-й и 2-й род проистекает из знака поверхностной энергии границы раздела «сверхпроводник — нормальный металл». Очевидно, что здесь возможны только два случая (вариант с нулем исключается): либо поверхностная энергия положительная, либо отрицательная. Поэтому этот критерий не изменится даже для двухщелевого сверхпроводника. Именно такой довод приводится в статье Interface energy of two band superconductors, опубликованной в журнале Physical Review B. Авторы работы, коллектив ученых из США и ЮАР, фактически проделали те же расчеты, что и Абрикосов, но для сверхпроводника с двумя сортами куперовских пар. Они показали, что в случае, когда для первого сорта куперовских пар параметр Гинзбурга–Ландау меньше 1/√2, а для второго он больше 1/√2, поверхностная энергия принимает положительное значение, а потому имеет место сверхпроводимость 1-го рода.

Более того, те же ученые в другой своей статье доказывают, что различие между двумя разновидностями куперовских пар в температурном диапазоне в окрестности Tc, то есть там, где применяется теория Гинзбурга–Ландау, исчезает, и двухщелевой сверхпроводник превращается в сверхпроводник с одной щелью.

Чего ожидать дальше?

Все описанные здесь работы носят исключительно теоретический характер и основываются на численном анализе теории Гинзбурга–Ландау. Поставить точку в этом споре могут лишь очень аккуратные эксперименты по наблюдению вихревой решетки в двухщелевых сверхпроводниках. Благо сейчас стало известно, что не только диборид магния обладает двумя сортами куперовских пар, но и недавно открытые железосодержащие сверхпроводники (см. Открыт новый тип высокотемпературных сверхпроводников, «Элементы», 12.05.2008 и Найдено новое семейство сверхпроводников, содержащих железо, «Элементы», 31.10.2008), высококачественные монокристаллы которых синтезировать немного проще. Так что теперь с большой вероятностью следует ждать возврата дискуссии в экспериментальную плоскость.

Источники:

1. V. H. Dao, L. F. Chibotaru, T. Nishio, V. V. Moshchalkov. Giant vortices, vortex rings and reentrant behavior in type-1.5 superconductors // arXiv:1007.1849 (12 July 2010).
2. Shi-Zeng Lin, Xiao Huy. Vortex States and Phase Diagram of Multi-component Superconductors with Competing Repulsive and Attractive Vortex Interactions // arXiv:1007.1940 (12 July 2010).
3. Egor Babaev, Johan Carlström, Martin Speight. Type-1.5 Superconducting State from an Intrinsic Proximity Effect in Two-Band Superconductors // Phys. Rev. Lett. 105, 067003 (5 August 2010).
4. Jani Geyer, Rafael M. Fernandes, V. G. Kogan, Jörg Schmalian. Interface energy of two band superconductors // Phys. Rev. B 82, 104521 (27 September 2010); также доступна как arXiv:1007.2794.
5. V. G. Kogan, J. Schmalian. Two-band superconductors near Tc // arXiv:1008.0581 (3 August 2010).

По материалам статьи Юрия Ерина: