Микроэлектроника переходит на квантовые точки // Нанофизика
Друзья, с момента основания проекта прошло уже 20 лет и мы рады сообщать вам, что сайт, наконец, переехали на новую платформу.
Какое-то время продолжим трудится на общее благо по адресу
На новой платформе мы уделили особое внимание удобству поиска материалов.
Особенно рекомендуем познакомиться с работой рубрикатора.
Спасибо, ждём вас на N-N-N.ru
На смену элементам электронных приборов, для которых применимо классическое описание, приходит элементная база наноэлектроники, где необходим последовательно квантовомеханический подход. Квантово-размерные наноструктуры важны не только для наноэлектроники, но и как основа информационных систем нового поколения, они могут применяться для создания магниточувствительных детекторов, на их основе в оптоэлектронике создаются сверхмалые лазерные источники.
Текст: Наталия Капуткина доктор физико-математических наук, НИТУ «МИСИС»
Михаил Алтайский доктор физико-математических наук, Институт космических исследований РАН
Современная субмикронная технология позволяет создавать объекты, в которых движение электронов локализовано в плоскости. Такая ситуация имеет место в полупроводниковых гетероструктурах, на переходе металл-диэлектрик. При приложении достаточно высокого напряжения перпендикулярно слоям гетероструктуры электроны выходят на поверхность и ведут себя как двумерный электронный газ. Если к тому же потенциал ограничивает электроны в одном направлении в плоскости, то электроны могут свободно двигаться только в одном оставшемся — это одномерный газ (квантовые проволоки). Если же ограничивается движение электронов в обоих направлениях, мы получаем квантовую точку.
 Рис. 01 Строение трехмерной квантовой точки
Рис. 01 Строение трехмерной квантовой точки
Декогеренция
Декогеренция — процесс нарушения когерентности, вызываемый взаимодействием квантовомеханической системы с окружающей средой. Можно сказать, что при декогеренции происходит потеря квантовых свойств системы.
Квантовые точки — искусственные атомы
Квантовые точки (КТ) — это гигантские (по сравнению с атомами) искусственные атомы с контролируемыми параметрами. Современные технологии позволяют получать и отдельные КТ, и массивы КТ с контролируемыми параметрами, такими как расположение, область локализации, число носителей заряда, крутизна удерживающего потенциала. Если мы сравним КТ и «обычные» атомы, то КТ перспективны из-за возможности управлять их свойствами с помощью магнитного поля таб. 01. Чтобы значимо изменить свойства обычных атомов, требуются поля, как в нейтронных звездах, а для квантовых точек — вполне доступные в земных лабораториях.
Системы же КТ могут рассматриваться как искусственные гигантские молекулы с контролируемо изменяемыми параметрам. Периодические и апериодические массивы КТ — искусственные кристаллы и квазикристаллы.
Таб. 01 Сравнение параметров квантовых точек и атомов
| параметр | атомы | квантовые точки |
| разность уровней энергии | 1 Эв | 10–4 Эв |
| энергия ионизации | 10 Эв | 10–4 Эв |
| управляющие магнитные поля | 104 Тл | 1–10 Тл |
Типичный размер квантовой точки — несколько десятков нанометров, однако размер занятой электронами области из-за внешнего потенциала может быть значительно меньше. В такой ситуации становится существенным квантование движения в плоскости границы, так что получается структура, подобная атому (с дискретными уровнями энергии), но роль атомного потенциала выполняет искусственно созданный потенциал квантовой точки, а число электронов может контролируемо изменяться от единиц до нескольких сотен.
В настоящее время наибольший интерес вызывают гетеронаноструктуры с квантовыми точками на основе арсенида галлия (GaAs) или его твердых растворов разного состава. Основное техническое применение квантово-размерных структур этого типа видится в настоящее время в разработках светоизлучающих приборов, прежде всего лазеров для волоконно-оптических линий связи. Также значительные возможности дает допирование структур на основе полупроводников переходными металлами.
Различие постоянных кристаллических решеток гетеропары, обычно считавшееся ее недостатком, оказалось весьма ценным свойством в технологии получения так называемых самоорганизованных квантовых точек. Под самоорганизацией понимается самопроизвольное возникновение упорядоченных макроскопических структур из менее упорядоченной среды. В основе процесса самоорганизации лежит свойство неравновесных физических систем при приближении к термодинамическому равновесию переходить в состояние, в котором свободная энергия системы минимальна.
Алгоритм Гровера
Квантовый (то есть реализуемый на квантовом компьютере) алгоритм решения переборной задачи. Классические алгоритмы требуют экспоненциального времени, алгоритм Гровера эффективнее, он требует логарифмического времени. Автор — американский математик индийского происхождения Лов Гровер (Lov Kumar Grover).
Если на поверхности из материала А осажден тонкий однородный слой материала В, то при установлении термодинамического равновесия в слое В возникает атомная структура, и он имеет форму, при которой свободная энергия системы будет минимальна. Факторами, определяющими направление и конечный результат самоорганизации, являются рассогласование постоянных решеток материалов А и В, создающее упругие напряжения в системе и повышающее ее внутреннюю энергию, толщина слоя и некоторые другие. При одних значениях этих параметров может образоваться однородный слой материала В, повторяющий структуру подложки. При других значениях может оказаться более энергетически выгодным, чтобы материал В образовал массив напряженных кластеров определенных размеров и формы или собрался в один большой кластер.
Экспериментально уже давно установлено, что при осаждении из паровой фазы наблюдаются три типа начальной стадии роста слоя на подложке:
1) послойный (двумерный) рост. Он происходит, если материал В смачивает подложку и его постоянная решетки мало отличается от постоянной решетки материала А;
2) островковый (трехмерный) рост слоя. Он имеет место при плохом смачивании;
3) промежуточный механизм роста, при котором сначала происходит послойный рост слоя В, который затем сменяется островковым ростом. Этот механизм наблюдается при наличии смачивания и значительном рассогласовании решеток А и В.
Последний механизм используется для получения самоорганизующихся квантовых точек в системе InGaAs/GaAs. Самый важный результат изучения данного механизма — возможность получения массива однородных по размерам, бездефектных, напряженных нанокластеров InGaAs в матрице GaAs, обладающих свойствами квантовых точек.
Часто применяется получение массивов квантовых точек с помощью молекулярно-лучевой эпитаксии, основанное на использовании самосогласованного роста по механизму Странского-Крастанова. Но квантовые точки, полученные в таком процессе, оказываются значительно напряженными. Это приводит к существенным сдвигам спектра электронных состояний и к изменению управляющих параметров.
В зависимости от условий создания квантовых точек могут быть использованы различные виды представления удерживающего потенциала.
Для круглой квантовой точки возможно представление потенциала в виде:
Это достаточно адекватно для не слишком больших квантовых точек. Для больших квантовых точек адекватна модель «жестких стенок». Но и в том, и в другом случае получается дискретный энергетический спектр, как у атома.
Возможности управлять состоянием отдельных квантовых точек и систем квантовых точек и методы воздействия, схематически изображены на рисунке 03.
Квантовые точки активно применяются в различных полупроводниковых лазерах, детекторах излучения, дозиметрах, биосенсорах, солнечных батареях и т.д.
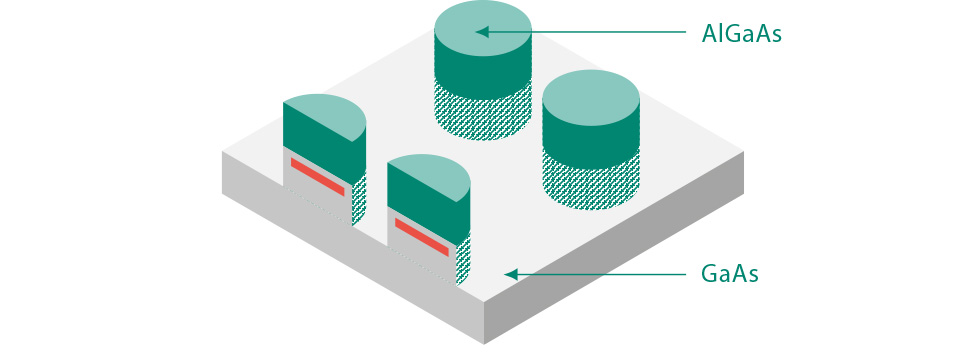 Рис. 03 Изменения состояния системы
Рис. 03 Изменения состояния системы

Квантовые точки в квантовых компьютерах
В последнее время возрос интерес к квантовым точкам в качестве элементной базы наноэлектроники, для мало- и одноэлектронных транзисторов, элементов памяти, в том числе с возможностью иерархического доступа, кубитов и логических вентилей.
Идеи квантовой механики входят в теорию вычислительных систем двумя путями. Во-первых, квантовые вычислительные алгоритмы, благодаря заложенному в них параллелизму, основанному на суперпозиции квантовых состояний, могут решать классические неполиномиальные задачи за полиномиальное время. Во-вторых, миниатюризация элементной базы компьютеров приводит к необходимости учета конечной, но отличной от единицы, вероятности перехода отдельных битов между состояниями «0» и «1» и конечной вероятности влияния этих переходов на состояние соседних битов.
Кандидатом на роль квантовой ячейки памяти в наноэлектронных устройствах, стабильной на практически значимых временах миллисекундного порядка, может быть кубит на основе электронных состояний квантовой точки. Основное состояние спина электрона в изолированной КТ может быть надежно приготовлено с помощью оптической накачки, или же с помощью тепловой релаксации в магнитном поле. Время декогеренции спина в КТ имеет порядок микросекунд, и спиновый кубит на основе КТ является перспективным элементом хранения и обработки квантовой информации.
В реальных вычислительных устройствах и устройствах квантовой памяти необходимо манипулировать не с отдельным кубитом, а с регистром из кубитов. Такие регистры могут быть построены, например, в виде массива КТ, отделенных друг от друга расстоянием, меньшим оптической длины волны. Непосредственная адресация к отдельному кубиту в таком массиве меняет состояние других кубитов и приводит к декогеренции. Однако возможно применить (Altaisky, Kaputkina IJQI 10, (2012), 1250026; arxiv.org:1105.1464) алгоритм иерархической записи информации в блоки из кубитов, реализованных на основе КТ, не использующий адресации к отдельным кубитам, а изменяющий состояние регистра как целого.
Квантовый компьютер
Это компьютер, базовая ячейка которого имеет квантовую природу, то есть может находиться не в одном из N дискретных состояний (обычно N=2), а сразу в их суперпозиции. Идея квантовых вычислений была высказана в начале 1980-х советским математиком Юрием Маниным и американским физиком Ричардом Фейнманом (Richard Phillips Feynman). Квантовый компьютер требует для выполнения стандартных операций иных, чем у классического, алгоритмов.
Достоинствами КТ в качестве элементной базы наноэлектроники являются миниатюрность, возможности контроля уровней энергии, заряда и формы КТ, масштабируемость (наличие технологии, позволяющей собирать КТ в массивы), — а также возможность оптического приготовления/измерения состояний отдельных КТ. Недостатком КТ в качестве элементов сетевого квантового компьютера является неизбежность взаимодействия с фононами гетероструктуры, на которой реализованы КТ, и, как следствие, небольшие времена декогеренции. По этой причине известные алгоритмы сетевого квантового компьютинга — факторизация (разложение на простые множители) по Шору и поиск в неупорядоченной базе данных по Гроверу — пока реализованы на других квантовых системах — ионах в ловушках и системах с ядерным магнитным резонансом. Эти системы, в отличие от КТ, позволяют добиться почти полной изоляции от окружения, но требуют больших затрат и не являются масштабируемыми.
Ситуация качественно изменилась примерно с 2011 года, когда компания D-wave Systems Inc. выпустила на рынок первые адиабатические квантовые компьютеры D-wave 1 («Rainer») на 128 кубит и D-wave 2 («Vesuvius») на 512 кубит (Johnson et al. Nature 473, (2011), 194). Отличие адиабатического компьютера от сетевого компьютера состоит в том, что ключевым его элементом является не унитарная эволюция начального состояния системы кубитов через систему квантовых гейтов к конечному состоянию (решению задачи), а процесс квантового туннелирования из приготовленного начального состояния в состояние, реализующее минимум энергии некоторого гамильтониана. Фактически было реализовано квантовое решение задачи поиска минимума квадратичной формы. К данному типу относится огромный класс задач в теории автоматического управления, экономике, распознавании образов. Их решение на квантовом адиабатическом компьютере может быть получено за полиномиальное время, в то время как на обычных компьютерах требуется экспоненциальное. При этом использование процесса квантового туннелирования не накладывает жестких ограничений на взаимодействие с окружением и по сути позволяет проводить вычисления в открытой квантовой системе.
Алгоритм Шора
Алгоритм факторизации целого числа (то есть разложения его на простые множители) при помощи квантового компьютера. Алгоритм требует полиномиального времени. Разработан американцем Питером Шором (Peter Shor) в 1994 году. Классический (то есть без квантового компьютера) алгоритм факторизации требует экспоненциального времени.
Квантовые точки в искусственном интеллекте
Квантовые нейронные сети привлекли к себе внимание, когда Google и NASA анонсировали использование процессоров D-wave Systems Inc. для задач искусственного интеллекта и классификации больших данных, с огромным финансированием соответствующих проектов. Создание квантовых систем искусственного интеллекта, безусловно, является приоритетным направлением исследований для любой индустриально развитой державы. По сути, такой интеллект должен заменить человека при принятии решений в многофакторных оптимизационных задачах, с которыми обычные компьютеры не могут справиться в силу экспоненциальных затрат времени. Прежде всего это относится к задачам автономного управления летательными аппаратами, задачам медицинской диагностики, управлению сложными техническими системами.
Квантовые точки могут оказаться полезными при создании квантовых нейронных сетей. Использование молекул квантовых точек на основе GaAs для построения квантовой нейронной сети было впервые предложено Элизабет Берман с соавторами в 2001 г. Данная идея в ее оригинальной форме, предполагавшей использование фононов подложки для управления сетью, практически нереализуема из-за сложностей, связанных с управлением спектром фононов и с его нестабильностью. Нами разрабатывается методика построения квантовой нейронной сети на основе квантовых точек с диполь-дипольным взаимодействием (Алтайский, Капуткина, Крылов ЭЧАЯ 45, (2014), 1824) и проводятся численные расчеты перепутывания состояний в такой системе при ненулевых температурах.
- Источник(и):
- Войдите на сайт для отправки комментариев
 Сайт о нанотехнологиях #1 в России
Сайт о нанотехнологиях #1 в России