Доказательство отмечает конец эпохи в изучении трёхмерных форм.
Тридцать лет назад математик Уильям Тёрстон [William Thurston] рассказал о своём видении: систематизации всех возможных конечных трёхмерных форм.

Тёрстон, обладатель Филдсовской премии, проведший большую часть карьеры в Принстонском и Корнеллском университетах, имел сверхъестественную способность представлять непредставимое: не только формы, живущие в обычном трёхмерном пространстве, но и гораздо больший зверинец форм, обладающих такими сложными свойствами, что они могут вместиться только в пространство с большим количеством измерений. Там, где другие математики видели зачатки форм, Тёрстон видел структуры: симметрии, поверхности, взаимосвязь между разными фигурами.

Уильям Тёрстон в Беркли в 1991 году.

«У многих людей после многих лет обучения складывается впечатление, что математика – это строгий и формальный предмет, занимающийся сложными и непонятными правилами,– писал он в 2009-м. – Хорошая математика являет собой полную противоположность этому. Математика – это искусство человеческого понимания… Математика поёт, когда мы чувствуем её всем мозгом».

В основании видения Тёрстона находился брачный союз между двумя, на первый взгляд, несопоставимыми подходами к изучению трёхмерных фигур: геометрией, знакомым царством углов, длин, областей и объёмов, и топологией, изучающей свойства формы, не зависящие от точных геометрических измерений – свойства, не меняющиеся, если форму растянуть или перекрутить, как " хэндгам ".

Для тополога поверхность сковородки эквивалентна поверхности стола, карандаша или мяча; поверхность кружки эквивалентна пончику, или тору. С точки зрения тополога многообразие двумерных форм – поверхностей – сводится к простому списку категорий: сферические, тороидальные, и тороидоподобные с большим количеством отверстий. (Большинство из нас представляют сферы и торы трёхмерными, но поскольку математики думают о них как о полых поверхностях, они считают эти поверхности двумерными объектами, измеряемыми площадью поверхности, а не объёмом).

Ключевой идеей Тёрстона было то, что понять 3-многообразияможно через объединение геометрии и топологии. Точно так же, как топологическая категория 2-многообразий, содержащая поверхности сковородки и карандаша, содержит также и идеальную сферу, Тёрстон предположил, что многие категории 3-многообразий содержат один экземпляр, 3-многообразие, чья геометрия настолько однородна и идеальна, настолько красива, что, по выражению Уолтера Ньюманна [Walter Neumann] из Колумбийского университета, она «звенит, как колокольчик». Более того, Тёрстон предположил, что формы, не имеющие такого экземпляра, можно порезать на кусочки, у которых он уже будет.

В работе от 1982 года Тёрстон выдвинул свою «гипотезу геометризации» в числе 23 вопросов о 3-многообразиях, предлагавших математикам направление познания трёхмерных форм. (В списке было 24 вопроса, но один из них, всё ещё не разрешённый, больше напоминает интригующий переулочек, чем основную дорогу).

«У Тёрстона был огромный талант задавать правильные вопросы,– говорит Владимир Маркович, математик из Калтеха. – Задавать вопросы могут все, но редко случается, что вопрос приводит к озарениям и красоте, так, как это удавалось вопросам Тёрстона».

Вопросы вдохновили новое поколение математиков, десятки которых решили вести свои работы под руководством Тёрстона. Его математические «детки» выражают его стиль, как писал Ричард Браун из Университета им. Джона Хопкинса. «Они смотрят на математику, как дети на ярмарку: с радостью и удивлением, очаровываясь каждым новым открытием, и они просто счастливы быть частью всего этого».

Десятки лет после появления работы Тёрстона математики следовали его «карте» исследований, и их мотивация питалась не столько возможными применениями их открытий, сколько удачным местом, которое 3-многообразия занимали в изучении форм. Двумерные формы довольно банальны, их легко изобразить и поделить на категории. Четырёх-, пяти-, и более многомерные формы вообще практически не поддаются дрессировке: разнообразие возможностей так велико, что математики ограничились познанием лишь их специальных подклассов. А в случае трёхмерных форм структуры, с одной стороны, загадочны и трудны, но с другой – принципиально познаваемы.

Работе Тёрстона минуло уже 30 лет, и все вопросы, кроме четырёх, уже разрешены, включая гипотезу геометризации, доказанную русским математиком Григорием Перельманом в 2002 году, что стало знаковым достижением современной математики. Но четыре оставшихся задачи упорно сопротивлялись.

«То, что мы так долго не можем их решить, означает, что там спрятано нечто очень глубокое»,– сказал Яйр Мински [Yair Minsky] из Йельского университета.

Наконец, в марте 2012 года Ян Эйгол из Калифорнийского университета в Беркли, всполошил математическое сообщество, объявив о доказательстве " гипотезы Вайза) ", закрывшей последние четыре вопроса Тёрстона одним махом.

Математики называют этот результат концом эпохи.

«Видение 3-многообразий, описанное Тёрстоном в его работе, в то время могло выглядеть фантастически, а теперь оно полностью осознано,– говорит Дэнни Калегари [Danny Calegari] из Калтеха. – Его представления были удивительным образом доказаны – и каждая деталь оказалась правильной».

«Мне казалось, что существует особое знание и особые методы мышления, свойственные мне одному,– писал Тёрстон, получив математическую премию Стила всего за несколько месяцев до смерти в августе 2012 в 65 лет. – И я очень рад, что достиг такого уровня, когда это не так – многие люди разделили мой способ мышления, и многие доказали теоремы, за которые я безуспешно брался».

Достижение Эйгола показывает существование простой схемы построения всех компактных гиперболических 3-многообразий – единственного типа трёхмерных форм, который ещё не был полностью объяснен.

«Мы теперь точно понимаем, как выглядят все 3-многообразия,– говорит Генри Уилтон [Henry Wilton] из Лондонского университетского колледжа. – Это кульминация огромной математической истории успеха».

Поверхностное изучение

Программа Тёрстона пыталась сделать с 3-многообразиями то, что математики успешно проделали уже сто лет назад с двумерными многообразиями. Чтобы размяться перед пониманием трёхмерных многообразий, заглянем во внутренности классификации «компактных ориентируемых» поверхностей (конечных поверхностей без проколов и надрезов с постоянной ориентацией).

Чтобы подойти к задаче классификации, математики показали, что для любой поверхности можно провести её последовательное упрощение, разрезая её вдоль кривых, пока она не раскроется в плоский полигон.

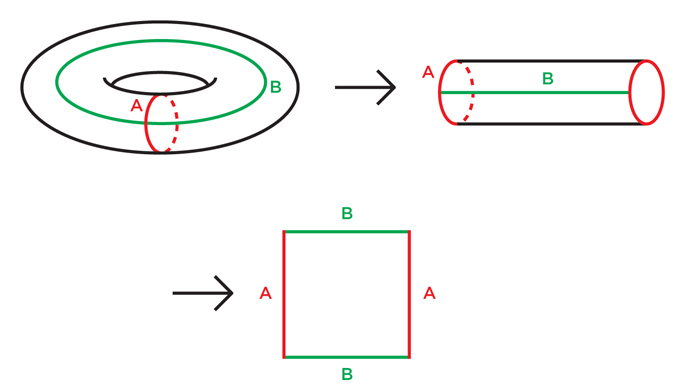
Рис. 1

Легко показать это для тора: сначала режем его по петле А, как на рис.1, получаем цилиндр. Затем режем по петле В, расправляем цилиндр в квадрат. Немного сложнее разобраться с рис.2, но и там резка по четырём кривым превращает двойной тор (тор с двумя отверстиями) в восьмиугольник. Таким же образом для любого тора с n отверстиями мы можем сделать надрезы по петлям количеством 2n и расправить его в 4n-угольник.

Рис.2

Произвольную неопределённую поверхность можно попробовать упростить (и идентифицировать её), разрезая её схожим образом. Если это не сфера, топологи показали, что в ней должны содержаться внутренние петли (петли, не пересекающие друг друга), которые нельзя стянуть в одну точку – такие, как А и В на торе. Разрезка поверхности по одной из этих петель удаляет несколько интересных топологических свойств поверхности. Математики показали, что для низведения поверхности до плоского многоугольника необходимо разрезать её конечное число раз.

Упростив поверхность до уровня многоугольника, просто видеть, что если мы склеим его края, чтобы восстановить изначальную поверхность, нам придётся изготовить тор, или двойной тор, или тройной тор и т.п. Ведь первая склейка превратит многоугольник в поверхность вида туннеля, а каждая последующая либо добавит новый туннель, или просто зашьёт открытые части. Когда мы закончим процесс, мы получим тор с некоторым количеством отверстий.

Такой подход не просто демонстрирует топологическую эквивалентность поверхности сфере или какому-нибудь тору: он также даёт способ наделить поверхность простой и единообразной геометрической структурой.

У сферы, очевидно, уже есть унифицированная геометрическая структура: её геометрия выглядит с любого места сферы одинаковой. Поверхность пончика, напротив, вовсе не единообразная: район внешнего края пончика загибается похожим на сферу образом, а район на внутреннем кольце загибается, как седло.

И как бы вы ни расположили тор в пространстве – неважно, как вы его будете растягивать и крутить – у вас не получится сделать так, чтобы в любом его месте геометрия была одной и той же. Некоторые части будут закругляться, как сфера, некоторые – как седло, некоторые могут быть плоскими.

Возможно, тем не менее, снабдить тор абстрактной геометрической структурой, идентичной в любой точке – просто объявить, что на каждом из мелких участков тора расстояния и углы определяются измерениями квадрата, из которого, как мы видели, можно сделать тор. Физический тор в обычном пространстве, длины и углы которого соответствуют этому абстрактному правилу, построить не получится, но это определение длин и углов внутренне непротиворечиво. Поскольку у квадрата обычная плоская (евклидова) геометрия, мы скажем, что тор можно снабдить евклидовой структурой. Тор, обладающий такой геометрией, напоминает видеоигру, в которой персонаж, исчезая с левой стороны экрана, вновь появляется на левой, а исчезая с верхней стороны, появляется на нижней.

Попытавшись проделать эту операцию с двойным тором, мы столкнёмся с препятствием. Помните, что мы можем сделать двойной тор, склеивая края восьмиугольника. Если мы объявим, что геометрия двойного тора должна копировать геометрию восьмиугольника, мы столкнёмся с проблемой его углов. После склейки восьмиугольника в двойной тор угловые точки будут склеены вместе, в одну точку двойного тора. В этой точке будут встречаться восемь углов, каждый будет добавлять по 135 градусов, что вместе составит 1080 градусов вместо 360.

Если мы попробуем придать двойному тору геометрическую структуру восьмиугольника, получится, что наш двойной тор будет обладать обычной евклидовой геометрией везде, кроме одной точки, где его поверхность выпячивается как остроконечная шляпа (угловые точки – не проблема, если мы склеиваем квадрат в тор: мы склеиваем четыре прямых угла и получаем идеальные 360 градусов).

Чтобы получить плавную геометрическую структуру в угловой точке двойного тора, нужно, чтобы каждый из восьми углов вносил только 45 градусов вместо 135. Интересно, что такой восьмиугольник существует, но живёт не в обычной евклидовой плоскости, а на другой структуре, называемой гиперболическим диском: третий тип геометрии, единообразной и внутренне непротиворечивой, как сферическая или евклидова. Но поскольку его сложнее представить, он был открыт математиками лишь в начале XIX века.

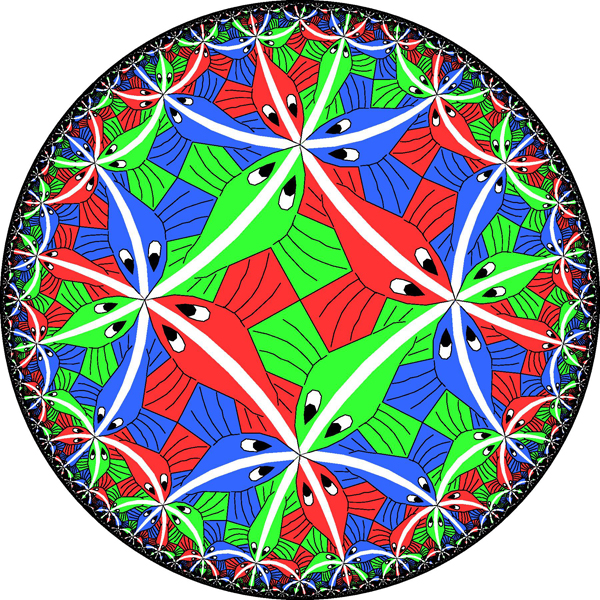Рис.3

Грубо говоря, гиперболическая геометрия (или геометрия Лобачевского) получается, если объявить, что все рыбы на рис.3 одного размера. Можно представить, что рис.3 на самом деле представляет собой изображение диска, полученное через искажающую линзу, которая делает рыб, находящихся ближе к краю, меньше, чем рыб в середине. На настоящем гиперболическом диске, находящемся перед линзой, все рыбы одного размера.

В обычном пространстве невозможно сделать правильный и гладкий гиперболический диск, чтобы все рыбы действительно были одинаковыми. Но с абстрактной точки зрения правило размера рыб даёт геометрию, которая внутренне непротиворечива и выглядит одинаково в любой точке – не для наблюдателя с искажающей линзой, а с точки зрения жителя гиперболического диска.

В гиперболической геометрии самый короткий путь, или «геодезическая», между двумя точками – это путь, проходящий через минимально возможное количество рыб. Такой путь – всегда полукруг, перпендикулярный границе диска. Примерами служат полукруги, проходящие по позвоночникам рыб. С нашей искажённой точки зрения эти пути искривлены, но для жителя диска это прямые линии. Как говорил Тёрстон, чтобы проехать по нему, не нужно поворачивать руль. В отличие от евклидовой плоскости, на которой параллельные линии всегда остаются на одном расстоянии, на гиперболическом диске две непересекающиеся линии могут очень быстро разойтись друг от друга.

С точки зрения гиперболической геометрии фигуры с рис.4 представляют собой обычные восьмиугольники с прямыми сторонами. В одном из этих восьмиугольников все углы по 45 градусов – как раз то, что нам нужно для двойного тора. Если мы правильно склеим стороны этого восьмиугольника, то получим двойной тор с идеальной и единообразной гиперболической структурой.

Тем же образом мы можем снабдить тройной тор гиперболической структурой. Тройной тор можно склеить из 12-угольника, так что если мы сделаем гиперболический 12-угольник с внутренними углами по 30 градусов, его гиперболическую геометрию можно плавно перенести на тройной тор. Продолжая тему, мы можем снабдить тор с 4 отверстиями, с 5-ю и так далее, гиперболической геометрией. Наша классификация компактных поверхностей получается следующей: одна поверхность со сферической геометрией (сфера), одна с евклидовой (тор), и бесконечно много поверхностей с гиперболической геометрией (все торы с количеством отверстий больше одного).

За последние сто лет эта классификация дала математикам весьма плодотворный метод переноса топологических вопросов о поверхностях в геометрическую область, и обратно. Классификация поверхностей – основная идея при изучении двумерных форм, открытие, используемое всеми остальными исследованиями в качестве отправной точки.

Следующее измерение

3-многообразия гораздо разнообразнее 2-многообразий, и задачи с ними сложнее. Даже простой на вид вопрос вроде знаменитой гипотезы Пуанкаре – которая спрашивает, является ли трёхмерная версия сферы единственной компактной трёхмерной формой, на которой каждую петлю можно стянуть в одну точку, не зацепившись за отверстие – оставался нерешённым почти сто лет после его постановки Анри Пуанкаре в 1904 году.

Но Тёрстон смело предположил, что возможно создать классификацию трёхмерных форм аналогично существующей классификации двумерных.

Двумерные евклидова, сферическая и гиперболическая геометрии обладают парами в трёх измерениях. Но в трёх измерениях список «красивых» геометрий ими не ограничивается. Существуют гибридные геометрии, являющиеся гиперболическими или сферическими в определённых направлениях и евклидовыми в других. В целом есть восемь различных видов геометрий в трёх измерениях, однообразных в том смысле, что геометрия выглядит одинаково в любой точке пространства.

Тёрстон предположил, что, как и с поверхностями, 3-многообразия можно сопоставить с естественными геометрическими структурами. Конкретно он предложил, что если вы разрежете любое компактное 3-многообразие на кусочки особым образом, каждый кусочек можно сопоставить с одной из восьми геометрий.

«Целью было полностью унифицировать топологию и геометрию в трёх измерениях»,– говорит Мински.

Естественным подходом к этой «гипотезе геометризации» было опробовать нечто похожее на то, что мы делали с поверхностями, которые мы резали по кривым, пока у них не вскрывались все интересные топологические свойства, и пока они не упрощались до плоского многоугольника. Для 3-многообразий похожим подходом будет резка их вдоль поверхностей, пока, будем надеяться, они не упростятся до многогранника, противоположные стороны которого можно склеить для получения изначальной формы. И если мы сможем построить этот многогранник при помощи правильной геометрии, мы можем преобразовать эту геометрию к изначальной форме, как это было с поверхностями.

Помните, что в случае поверхностей каждая кривая должна была удовлетворять двум требованиям: кривая не пересекается с собой (математики говорят, что она должна быть «встроенной»), и она должна быть, как мы это называем, топологически интересной, то есть, окружать некую топологическую деталь поверхности так, чтобы её нельзя было стянуть в точку (это требование гарантирует, что резка вдоль этой кривой упрощает топологию поверхности).

В 1962 году математик Вольфганг Хакен [Wolfgang Haken] доказал, что 3-многообразие можно упростить до многоугольника, если 3-многообразие содержит поверхность, разрез по которой удовлетворяет двум условиям: она должна быть встроенной и «несжимаемой», то есть, любая топологически интересная кривая на поверхности будет также топологически интересной в более общем контексте окружающего 3-многообразия.

К примеру, тор не будет несжимаемым в обычном трёхмерном пространстве, поскольку петля, проходящая через отверстие тора, топологически интересна с точки зрения поверхности тора, но в трёхмерном пространстве её можно сжать до одной точки. И наоборот, тор несжимаем внутри 3-многообразия, которое можно получить, утолщив поверхность тора так, чтобы он перестал быть бесконечно тонким. Для того, чтобы быть несжимаемой, каждая топологическая особенность поверхности должна отражать какую-либо внутреннюю топологию 3-многообразия. Теперь 3-многообразие, у которого есть встроенная несжимаемая поверхность, называется многообразием Хакена.

Если наше 3-многообразие обладает встроенной несжимаемой поверхностью, то резка вдоль неё вскроет некоторые интересные топологии, и даст нам упрощённое многообразие. Более того, Хакен показал, что если в многообразии содержится одна такая поверхность, то новое многообразие, полученное резкой вдоль неё, также будет многообразием Хакена: у неё тоже будет встроенная несжимаемая поверхность для резки. И после конечного числа таких шагов, как показал Хакен, все интересные топологические особенности изначального многообразия будут отрезаны, и останется простой многогранник.

В конце 1970-х Тёрстон показал, что возможно снабдить получившийся многогранник одной из восьми трёхмерных геометрий таким образом, что она плавно переносится на вновь склеенный многоугольник, идеально состыковываясь на углах и рёбрах многогранника. Иными словами, Тёрстон доказал свою гипотезу геометризации для тех многообразий, стандартная декомпозиция которых приводит к получению кусочков, являющихся многообразиями Хакена.

К сожалению, для произвольного компактного 3-многообразия гарантий наличия у него такой поверхности нет. В конце 1970 – начале 1980-х, Тёрстон убедил сообщество, что 3-многообразия, содержащие встроенную несжимаемую поверхность (многообразия Хакена) являются исключениями, а не правилами.

Поиски доказательства гипотезы геометризации для многообразий, отличных от многообразий Хакена, застопорило математиков больше, чем на двадцать лет. Наконец, в 2002 году Перельман представил своё доказательство, основанное на областях математики, далеко отстоящих от тех, что изучали большинство последователей Тёрстона. (Походя доказательство Перельмана задело и столетнюю гипотезу Пуанкаре, что привело к тому, что математический институт Клэя предложил ему в 2010 году премию в миллион долларов – которую тот сразу отверг по сложным причинам).

Доказательство Перельмана стало поворотным пунктом, объединившим, как мечтал Тёрстон, топологию и геометрию. Теперь у каждой топологической проблемы, связанной с 3-многообразиями, есть геометрическая пара, и наоборот. Но теорема Перельмана оставила нерешённой множество важных вопросов о том, какие типы 3-многообразий могут существовать.

Классифицируя компактные 2-многообразия (поверхности), математики не только смогли показать, что каждую поверхность можно снабдить геометрической структурой, но и сделать полный список всех возможных 2-многообразий. В трёх измерениях такого списка сильно не хватало.

Семь из восьми трёхмерных геометрий – все, кроме гиперболической – были достаточно хорошо известны, и даже до работы Перельмана топологи составили полное описание типов многообразий, допускающих одну из этих семи геометрий. Эти формы сравнительно просты, и их мало.

Но, как и в случае поверхностей, в трёх измерениях оказалось, что большинство многообразий гиперболические. И охват огромного количества возможностей гиперболических 3-многообразий у математиков был гораздо худшим, чем для остальных семи геометрий.

«Из восьми типов геометрий гиперболические многообразия – самые загадочные и богатые»,– сказал Николя Бержерон [Nicolas Bergeron] из Университета Пьера и Марии Кюри в Париже.

Результат Перельмана сообщил математикам, что гиперболические многообразия были последним рубежом – единственным типом 3-многообразий, который осталось понять. Но он не сказал им, как выглядят эти гиперболические формы.

История с обложкой

И снова математики смогли обратиться к работе Тёрстона за наставлениями. В его знаменитом списке вопросов было множество гипотез о свойствах гиперболических 3-многообразий, включавших две гипотезы, напрямую относившиеся к их внешнему виду: «виртуальная гипотеза Хакена» и гипотеза «виртуального расслоения».

Виртуальная гипотеза Хакена (ВГХ) утверждает, что каждое компактное гиперболическое 3-многообразие почти что является многообразием Хакена в определённом смысле: возможно преобразовать многообразие в многообразие Хакена развёртывая его конечное число раз определённым способом. Это новое развёрнутое многообразие зовётся «конечным покрытием» изначального многообразия.

Математики говорят, что одно многообразие N покрывает другое многообразие M, если, грубо говоря, возможно обернуть N вокруг M определённое количество раз (возможно, и бесконечное) так, чтобы каждая часть M была покрыта столько же раз, как все остальные. Чтобы быть покрытием, это обёртывание должно обладать кучей других свойств – к примеру, N не должно загибаться на само себя, или рваться во время обёртывания. Каждый кусочек M покрыт кучкой его идентичных копий в покрывающем его N.

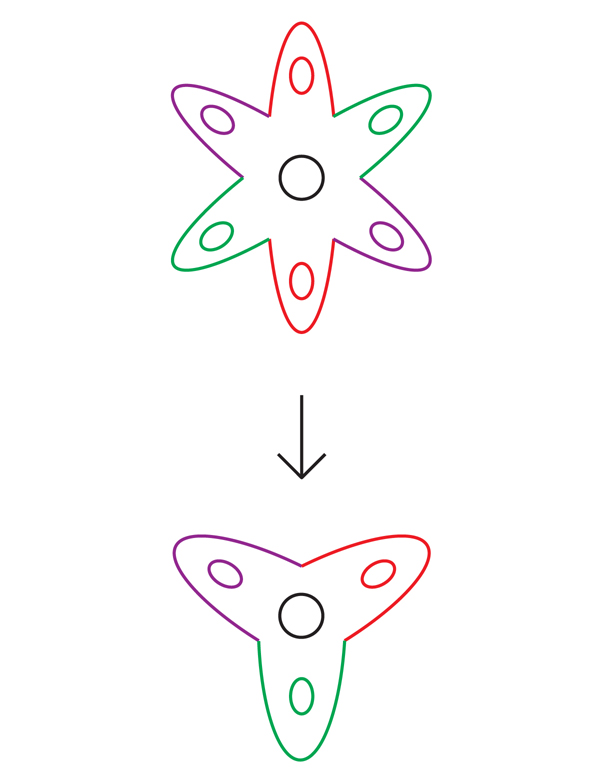Рис.5

К примеру, шестилепестковый цветок на рис.5 покрывает трёхлепестковый цветок: просто оберните шестилепестковый цветок два раза вокруг трёхлепесткового. Каждая точка трёхлепесткового цвета покрыта двумя точками шестилепесткового. Математики называют это двухслойным покрытием.

Точно так же бесконечный цилиндр покрывает тор: просто наматывайте цилиндр вокруг тора бесконечное количество раз (рис. 6). Каждая точка цилиндра покрыта: петля А покрыта бесконечным набором равномерно распределённых по цилиндру петель, а петля В разворачивается на цилиндре в линию, идущую вдоль.

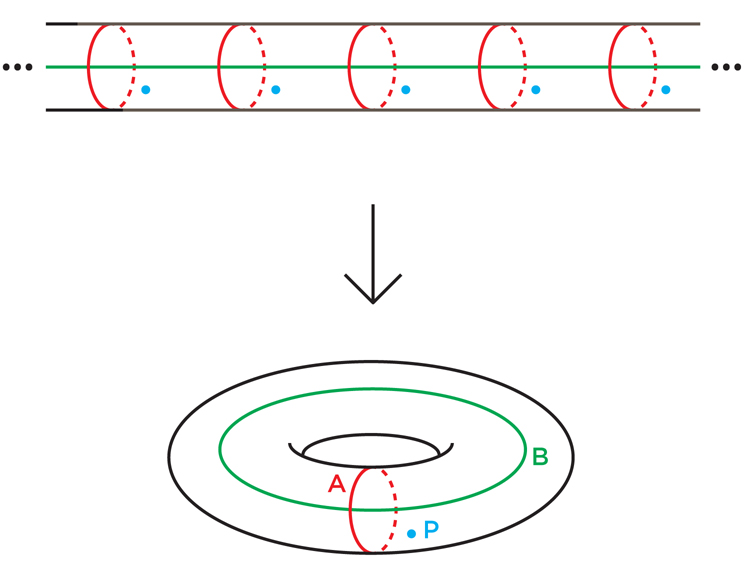Рис. 6

Топологии многообразия и его покрытия тесно связаны. Для воссоздания многообразия из n-слойного покрытия нужно просто сложить покрытие само с собой n раз. И наоборот, чтобы воссоздать покрытие на основе многообразия, вы разрезаете его, делаете n копий, и склеиваете вместе по границам (конкретное полученное вами покрытие зависит от выбора последовательности склейки).

Покрытие сохраняет некоторые топологические свойства многообразия, и открывает другие. Бесконечный цилиндр, к примеру, помнит, что петля А на торе закрытая, но забывает, что петля В также закрытая.

Этот процесс развёртывания и привёл Тёрстона к надежде, что для 3-многообразия возможно произвести покрытие с конечным количеством слоёв, которое будет многообразием Хакена. Мы уже указывали, что не следует ожидать, что произвольное компактное гиперболическое 3-многообразие будет многообразием Хакена (что у него будет встроенная несжимаемая поверхность). Но в 1968 году немецкий математик Фридхельм Волдхаузен [Friedhelm Waldhausen] предположил, что такое многообразие должно, по крайней мере, содержать несжимаемую поверхность, хотя она и может проходить сквозь себя, а не быть встроенной.

Если это так, утверждал Тёрстон, может существовать конечное покрытие, в котором поверхность разворачивается таким образом, который устраняет все самопересечения. Конечные покрытия часто упрощаются таким образом. К примеру, поскольку кривая в трёхлепестковом цветке на рис.7 обходит вокруг центрального отверстия дважды, никакие растягивания и сдвиги не могут заставить её не пересекаться с самой собой. Но если мы будем разворачивать эту кривую на шестилепестковом цветке, начав с определённой точки Р, результирующая красная кривая (которую математики называют «подъёмом» изначальной кривой) обойдёт вокруг центрального отверстия только один раз и не пересечётся с собой. (Есть и второй подъём, голубая кривая, пересекающая красную в двух точках, закрывающая точку пересечения в трёхлепестковом цветке).

Рис.7

В работе 1982 года Тёрстон предложил, что если у нас есть компактное гиперболическое 3-многообразие, должен быть способ развернуть его так, чтобы получить встроенные поверхности в конечном покрытии – то есть, 3-многообразие должно быть «виртуально Хакеновым».

Как мы уже видели, многообразие Хакена можно построить, склеивая границы граней многогранника определённым образом. ВГХ подразумевает, что любое компактное гиперболическое 3-многообразие можно построить, сначала правильно склеив многогранник, а затем обернув полученную форму вокруг себя конечное число раз.

Тёрстон сделал даже ещё более строгое предположение: что каждое компактное гиперболическое 3-многообразие может виртуально расслаиваться, то есть, иметь конечное расслоённое покрытие. Многообразие, которое «расслаивается над кругом» (как говорят математики), строится путём небольшого утолщения поверхности, что делает её трёхмерной, и склеивания внутренней и внешней границы вместе любым способом, обеспечивающим гладкое соединение поверхностей в каждой точке. (Такая склейка невозможна в обычном пространстве без пересечения частей результирующего многообразия друг с другом, но абстрактно его всё равно можно изучать). О расслоении многообразия говорят, потому что можно представить, как утолщённую поверхность растягивают так, чтобы граничные поверхности разошлись далеко друг от друга, а затем разворачивают и притягивают их навстречу друг другу перед склеиванием, и результирующее многообразие напоминает браслет с бесконечно тонкой бусиной в форме поверхности в каждой точке нити браслета. Эти бусины и есть слои.

Каждый расслоённое многообразие – это многообразие Хакена, но не наоборот. Поэтому, гипотеза о виртуальных расслоениях сильнее ВГХ, и Тёрстон не был уверен в том, что она правдива. «У этого сомнительного вопроса, судя по всему, есть определённый шанс получить положительный ответ»,– это всё, что он мог написать в работе 1982 года.

Изначально Тёрстон высказал ВГХ в ранней попытке подступиться к своей гипотезе геометризации, которую он уже доказал для 3-многообразий Хакена. Если ВГХ была верна, и каждое компактное 3-многообразие было конечным покрытием Хакена, то, возможно (надеялся Тёрстон), удастся использовать геометрическую структуру покрытия, чтобы построить геометрическую структуру изначального многообразия.

30 лет спустя, сильно позже того, как Перельман доказал гипотезу геометризации совершенно другими методами, ВГХ и гипотеза о виртуальном расслоении оставались недоказанными. Они вместе с двумя другими связанными с ними гипотезами оставались единственными вопросами без ответа из 23-х. Компьютерные подсчёты говорили в пользу правдивости ВГХ – конечные покрытия Хакена были найдены для каждого из перебранных компьютером 10 000 гиперболических 3-многообразий. Эту работу проделали Тёрстон и Нэйтан Данфилд [Nathan Dunfield] из Иллинойсского университета в Урбане-Шампейне. Но компьютерный перебор – это не доказательство.

«Когда Тёрстон выдвинул эту виртуальную гипотезу Хакена, этот вопрос казался лёгким. Но он упрямо сопротивлялся решению, что и пролило свет на то, как мало мы разбираемся в этой области,– сказал Мински. – Оказалось, что наше невежество в этом направлении было глубоким».

Строим поверхности

В 2009 году мутные воды, окружающие ВГХ, стали очищаться. В тот год Маркович и Джереми Кан [Jeremy Kahn], тогда работавший в Университете Стони Брук, объявили о доказательстве ключевого шага к доказательству ВГХ. Результат, который мы назовём «теоремой о несжимаемых поверхностях», постулирует, что каждое компактное гиперболическое 3-многообразие содержит несжимаемую поверхность (которая, возможно, пересекается с собой, и не является встроенной).

Доказательство Кана и Марковича – один из центральных примеров взаимодействия трёхмерной топологии и геометрии: теорема о несжимаемых поверхностях представляет собой чисто топологическое утверждение, но для его доказательства Кан и Маркович активно пользовались другой структурой, взятой из гиперболической геометрии.

Для постройки поверхности внутри 3-многообразия, Кан и Маркович использовали свойство гиперболических форм под названием «экспоненциальное смешивание». Это значит, что если вы начинаете путь где-то в малой области внутри многообразия, выбираете направление, и представляете, что ваша область начинает перемещаться по реке, текущей примерно в выбранном направлении, то ваша область постепенно распространится и обернётся вокруг 3-многообразия, доберётся до любого возможного места с любого возможного направления. Более того, оно сделает это очень быстро в точном «экспоненциальном» смысле.

Свойство смешивания уникально для гиперболических 3-многообразий и растёт, грубо говоря, из того факта, что в отличие от евклидовых пространств, в гиперболическом пространстве «прямые линии», или геодезические, искривляются друг относительно друга. Если вы выберете небольшую область гиперболического диска и позволите ей перемещаться в выбранном направлении, она экспоненциально быстро вырастет. Внутри компактного 3-многообразия растущая область тоже вырастет экспоненциально, но поскольку размер многообразия конечен, эта область в итоге будет оборачиваться вокруг него снова и снова, перекрывая себя много раз. Более того – а это уже сложнее доказать – область обернётся вокруг многообразия равномерно, проходя через все точки примерно с одинаковой частотой.

Математики разобрались с этим свойством экспоненциального смешивания уже более 25 лет назад и тщательно изучили статистику этого «геодезического потока», примерно выяснив, когда и как часто заданная область пройдёт по определённой точке. Но до тех пор, пока Кан и Маркович не взялись как следует за теорему несжимаемой поверхности, математики не могли использовать это свойство для построение топологических структур в многообразии (Ещё один математик, Льюис Боуэн [Lewis Bowen] из Техасского университета A&M пробовал использовать экспоненциальное смешивание для построения несжимаемых поверхностей в 3-многообразиях, но его работа наткнулась на технические препятствия).

Чтобы увидеть, как свойство экспоненциального смешивания помогает строить топологические и геометрические структуры, применим его к более простой задаче, чем построение поверхностей: построение замкнутой геодезической петли, чья длина близка к нашему любимому большому числу (обозначим его R).

Для построения петли, выберем любую начальную точку в многообразии и любое начальное направление, а затем включим воображаемый поливочный шланг, расположенный в небольшой области, включающей стартовую точку, и направим его грубо в выбранном направлении. Капли воды полетят вдоль геодезического пути, и пока R будет достаточно большим, смешивание потока будет означать, что к тому времени, когда капли пройдут расстояние R, они распределятся примерно равномерно по всему многообразию. В частности, по меньшей мере одна капля должна будет вернуться в район начальной точки. Затем мы просто построим небольшой мост, соединяющий геодезическую этой капли с начальной точкой, чтобы получить петлю, почти идеально геодезическую, с длиной примерно равной R. Несложно показать, что затянув эту петлю потуже на многообразии, можно получить идеальную геодезическую петлю.

Отметим, что метод даёт нам не одну-единственную геодезическую петлю, близкую к R. В этом процессе можно использовать любую начальную точку и любое направление, поэтому таких петель можно сделать много. Это основной принцип построения структур с использованием экспоненциального смешивания.

Экспоненциальное смешивание «утверждает, что какие бы структуры в многообразии вы не нашли, вы найдёте их в достаточном количестве»,– говорит Калегари.

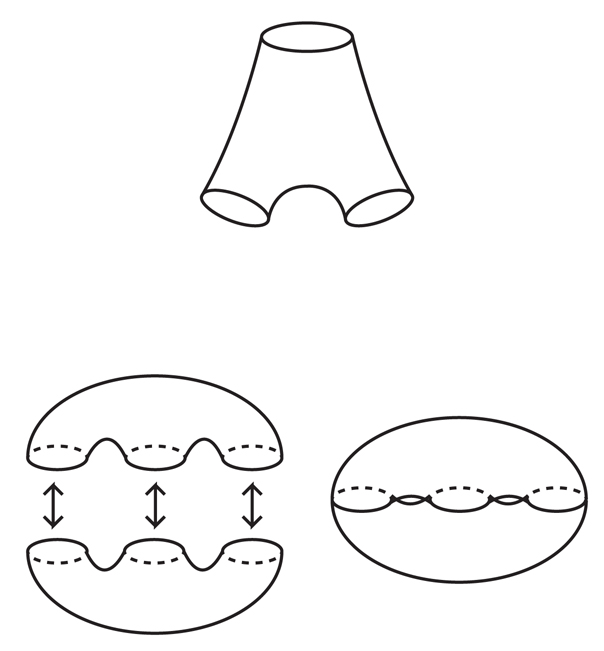Рис.8

Кан и Маркович использовали похожий на наше упражнение подход для создания «пар брюк» – поверхностей, топологически эквивалентных сфере с тремя отверстиями (так сказать, одно для пояса и два для ног). Эти брюки – исходный материал для построения всех компактных поверхностей, кроме сферы и тора – к примеру, склейка (или сшивание) двух брюк даёт нам двойной тор (рис.8).

Кан и Маркович показали, что для любого достаточно большого числа R возможно построить множество пар таких брюк внутри многообразия, что три их «манжеты» приблизятся длиной к R, и будут почти полностью геодезическими, то есть каждый кусочек поверхности брюк будет выглядеть практически одинаково с точки зрения гиперболической геометрии.

Также они показали, что для любой манжеты у брюк есть другая пара брюк, идущая от манжеты примерно в противоположном направлении. Сшивая вместе эти брюки у манжет, Кан и Маркович получили большое семейство компактных поверхностей, практически полностью геодезических, с небольшими морщинами у швов. Почти геодезические поверхности несжимаемы внутри их 3-многообразия, поэтому конструкция Кана и Марковича доказала теорему несжимаемых поверхностей.

Также этот метод показал, что у 3-многообразия есть не только одна несжимаемая поверхность, но «богатая структура почти геодезических поверхностей в разных местах»,– говорит Калегари.

Работа Кана и Марковича принесла им Премию Математического института Клэя 2012 года, вручаемую за математические прорывы.

«Техники Кана и Марковича не уступают по интересу их результатам, и эта работа, без сомнения, вдохновит множество других связанных с нею направлений исследований»,– предсказывал Джеффри Брок [Jeffrey Brock] из Брауновского университета в статье 2011 года.

Скрытая структура

Кан и Маркович создали начальную точку для математиков, пытающихся доказать ВГХ.

Они показали, что каждое многообразие гарантированно содержит несжимаемую поверхность. Но эта поверхность может проходить себя насквозь, возможно, что и во многих местах, а не быть встроенной. Чтобы на основе работы Кана и Марковича получить ВГХЮ математикам нужно было найти конечное покрытие многообразия, в котором, точно, как в примере с шести- и трёхлепестковыми цветами, поверхность поднимается до набора не пересекающих самих себя поверхностей (хотя они могут пересекать друг дружку). Если бы это было возможно, каждая из них была бы встроенной несжимаемой поверхностью в покрытии, и значит, покрытие было бы Хакеновым.

Но как найти такое покрытие?

«Между работой Кана и Марковича и ВГХ очень большой разрыв,– говорит Данфилд. – Их открытие было важным, но было непонятно, поможет ли оно в поиске встроенных поверхностей».

Работа Кана и Марковича привлекла внимание Дэниела Вайза [Daniel Wise] из университета Макгилла. Вайз сделал карьеру на исследованиях, посвящённых удалению самопересечений топологических объектов при помощи конечных покрытий, но он работал в контексте «кубических комплексов», объектов, на первый взгляд, сильно отличающихся от 3-многообразий. Работа Кана и Марковича помогла Вайзу показать другим математикам, что эти два контекста не так уж и различаются.

Кубический комплекс – он и есть кубический комплекс (КК): это набор кубов, только «кубом» там называется не только трёхмерный куб, но и форма в любом количестве измерений, состоящая из всех точек, координаты которых лежат, допустим, на отрезках между –1 и +1. К примеру, квадрат – это двумерный куб, а отрезок – одномерный. Кубы в КК соединены друг с другом вдоль углов, рёбер, граней и сторон высших измерений.

Рис.9

КК сильно отличаются от 3-многообразий – они даже не являются многообразиями, поскольку пересечения двух кубов разных измерений не напоминают обычное пространство любого из измерений. Но КК – упрощённые объекты, в которых изучают один ключевой аспект поверхности, содержащейся в 3-многообразиях: тот факт, что такая поверхность хотя бы локально делит её окружение на две части.

Если вам нужно исследовать объекты, делящие форму на две части, кубы – естественное поле для старта, поскольку из всех возможных форм у них есть простейший из подобных объектов: гиперплоскости, разрезающие их посередине. У квадрата есть две гиперплоскости (ГП) – вертикальная и горизонтальная линии, разрезающие его напополам. У куба – три ГП (см. Рис.9). У n-мерного куба n ГП, пересекающихся в его центре.

«Гиперплоскости сродни поверхностям в 3-многообразии, но вы мгновенно их видите,– говорит Вайз. – Искать поверхности тяжело, но гиперплоскости доступны вам с самого начала».

Если мы начнём с ГП внутри куба в КК, то найдётся ровно один способ расширить ГП до ГП в соседних кубах; после этого найдётся ровно один способ расширить их до соседних; и так далее. Поэтому, для каждой начальной ГП в КК есть уникальный способ расширения её до ГП во всём КК (см. рис.10).

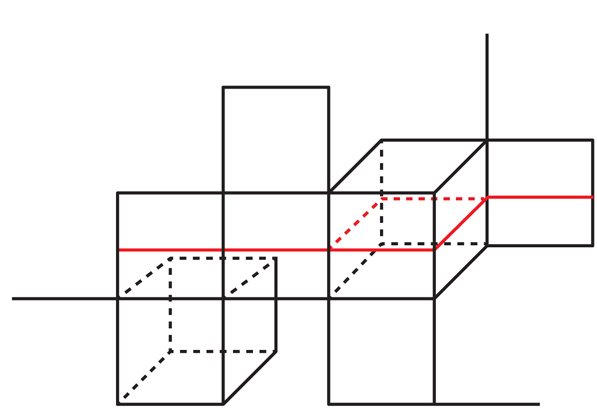Красная гиперплоскость в самом правом квадрате уникальным образом расширяется до гиперплоскости во всём кубическом комплексе.

Это качество сильно контрастирует с 3-многообразиями, в которых небольшой участок поверхности можно расширить до всей поверхности множеством способов. КК со своими ГП «красивые, кристально понятные и строгие»,– говорит Эйгол, и у них нет «дряблости» 3-многообразий и их поверхностей.

Когда мы расширяем ГП в КК, она может наткнуться на тот куб, с которого всё началось, и пройти через него перпендикулярно начальной ГП (см. рис.11). Иначе говоря, расширенная ГП не обязательно будет встроенной. Как в случае с поверхностями внутри 3-многообразий, можно спросить, есть ли у КК конечное покрытие, в котором эти самопересекающиеся ГП поднимаются до встроенных – это версия виртуальной гипотезы Хакена для КК.

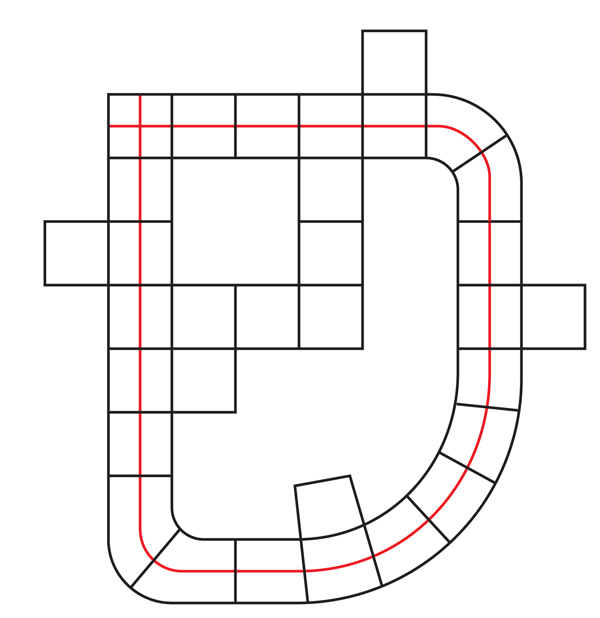Рис.11

Несколько лет назад Вайз и Фредерик Хаглунд [Frédéric Haglund] из Университета Париж-юг XI, определили класс «особых» КК, у которых, кроме других свойств, есть только встроенные ГП. В последнем десятилетии Вайз разработал арсенал техник, приспособленных для выявления «особых КК». В 2009 году Вайз выпустил 200-страничную «основную работу», как назвал её Данфилд, в которой он описал набор открытий, связанных с особыми КК, например «теоремы комбинаций», показывающие, как собрать воедино особые КК, чтобы гарантированно получить новые КК, также обладающие «особостью». В работе Вайз сформулировал гипотезу, утверждавшую, грубо говоря, что любой КК с геометрией, загибающейся образом, схожим с гиперболической геометрией, «виртуально» особый – то есть, у него есть особое конечное покрытие. Эту гипотезу назвали гипотезой Вайза.

Вайз был убеждён, что если данная форма определённым образом схожа с КК – когда её можно «кубировать» – то структура КК будет ключом к открытию множества свойств изначальной формы.

«КК был секретом, о котором люди даже не знали, что нужно спрашивать,– говорил он. – Это фундаментальная скрытая структура».

Кубические леса

Вайза чрезвычайно волновало кубирование форм, но сначала его коллеги смеялись над ним из-за этой мании.

Затем Кан и Маркович доказали теорему несжимаемой поверхности, и Вайз и Бержерон немедленно опубликовали работу, показывающую, что существование несжимаемых поверхностей в компактном гиперболическом 3-многообразии даёт метод его кубирования – да таким образом, что поверхности 3-многообразия точно соответствуют гиперплоскостям в результирующем кубическом комплексе.

Ключом к конструкции Вайза и Бержерона послужил тот факт, что Кан и Маркович показали, как сконструировать не одну, а множество поверхностей. Следуя подходу к кубированию, впервые сформулированному в 2003 года Майклом Сагеевым, сейчас работающим в Технионе (Израиль), Вайз и Бержерон начали с того, что взяли огромную коллекцию поверхностей Кана-Марковича – достаточно, чтобы разделить 3-многообразие на компактные многоугольники.

Теперь представим одну из точек пересечения этих поверхностей – допустим, в ней встречаются n поверхностей. Догадкой Сагеева было рассматривать это пересечение как тень, так сказать, от пересечения n гиперплоскостей в n-мерном кубе. КК, соответствующий 3-многообразию, строится, грубо говоря, добавлением одного n-мерного куба для каждого пересечения n поверхностей (реально всё это строится более тонко, чтобы учесть разные непредвиденные топологические обстоятельства). Два куба в комплексе соседние, если их соответствующие точки пересечения в 3-многообразии соединены гранью одного из многогранников.

«Кубический комплекс нужен, чтобы точно подсчитать, как поверхности пересекаются сами с собой и друг с дружкой»,– говорит Данфилд.

Вайз и Бержерон показали, что этот КК «гомотопно эквивалентен» изначальному многообразию, то бишь, КК можно сжимать и растягивать (с учётом сплющивания в некоторых измерениях и обратного процесса) до тех пор, пока КК не превратится в многообразие, и наоборот. Более того, эта гомотопная эквивалентность превращает каждую поверхность 3-многообразия в соответствующую гомотопно-эквивалентную ГП в КК.

Построенный таким образом КК удовлетворяет геометрическим требованиям гипотезы Вайза, что значит, что если гипотеза Вайза верна, то у этого КК существует конечное покрытие, в котором все ГП будут встроенными.

Если такое конечное покрытие в самом деле существует (допустим, покрытие m листами), то нужно вспомнить, что покрытие можно построить из самого КК, взрезав его особым образом, затем сделав m копий этого КК и склеив их вместе по линиям разрезов. Несложно показать, что этот рецепт изготовления покрытия можно перенести на изготовление конечного покрытия 3-многообразия, и что в этом конечном покрытии поверхности Кана-Марковича, использованные для построения КК, поднимутся до встроенных поверхностей. Иными словами, если гипотеза Вайза верна, то верна и ВГХ.

«Это очень странный компромисс: ваш КК может быть, к примеру, 10 000-мерный, и вам может показаться, что в каком-то смысле вы ухудшаете ситуацию,– говорит Вайз. – Но даже, несмотря на величину КК, многие его свойства очень легко понять, так что эта процедура очень ценная. Мы предпочитаем что-то большое, но хорошо организованное, вместо 3-многообразия».

Даже после того, как Вайз и Бержерон установили связь между КК и ВГХ, большинство топологов, изучающих 3-многообразия держались от КК подальше. Возможно, потому, что 200-страничная работа Вайза была обескураживающей, или потому, что КК настолько отличались от привычных им пространств.

«Эти идеи были слишком эзотерическими для людей, вышедших из гиперболической геометрии»,– говорит Бержерон.

Но один математик уже хорошо разбирался как в топологии 3-многообразий, так и в более абстрактных комбинаторных вещах, использовавшихся Вайзом в его подходе.

«Я думаю, Ян Эйгол был единственным спецом по 3-многообразиям, кто достаточно рано понял, как идеи Вайза можно использовать для топологии 3-многообразий»,– говорит Бержерон.

Эйгол углубился в изучение «главной работы» Вайза и убедился, что все её части, относящиеся к гипотезе Вайза, верны. Эйгол уже какое-то время занимался ВГХ; он понял, что подход Вайза, превративший дряблые поверхности в кристаллические гиперплоскости, был именно тем, что ему было нужно.

«КК даёт нам леса для строительства конечного покрытия»,– сказал он.

Чтобы построить особое конечное покрытие на КК Вайза-Бержерона, Эйгол начал нарезать КК вдоль ГП на «кубики Lego». Затем он назначил цвета граням блоков, так, чтобы у двух любых граней, встречающихся на углу, были разные цвета. Затем, Эйгол показал, что, грубо говоря, есть способ склеить конечное количество копий кубиков Lego вдоль граней с одинаковыми цветами таким образом, что цвета на сторонах этих граней тоже будут совпадать. В результате, каждая расширенная ГП будет одного цвета. Получившийся КК будет конечным покрытием изначального, и все его ГП будут встроенными, поскольку две любых пересекающихся ГП будут разного цвета, поэтому это не будет одна ГП, пересекающая сама себя.

12 марта Эйгол объявил о доказательстве гипотезы Вайза, а следовательно, и виртуальной гипотезы Хакена.

«Это были самые волнующие новости с тех пор, как Перельман доказал гипотезу геометризации»,– сказал Данфилд.

Информация прошла по сообществу исследователей 3-многообразий, и КК сразу же стали общей темой для всех топологов.

«Думаю, что до сих пор математическое сообщество не поняло, насколько мощна работа Вайза,– сказал Эйгол. – Думаю, что мой результат объяснит людям, какого удивительного прогресса он достиг».

Теперь, по словам Вайза, математики начинают понимать, что «каждый раз, когда ты что-нибудь кубируешь, ты сможешь раскрыть много всяких секретов структуры».

Конец эпохи

Доказательство Эйголом теории Вайза было доказательством «4 по цене 1»: оно доказало не только ВГХ, но и другие три из 23-х вопросов Тёрстона, до той поры остававшиеся открытыми. За время, предшествовавшее доказательству, Эйгол и другие математики показали, что все эти три вопроса – гипотеза виртуального расслоения и два более технических вопроса касательно гиперболических 3-многообразий – также вытекали из гипотезы Вайза.

В случае гипотезы виртуального расслоения вспомним, что целью было показать, что у каждого компактного гиперболического 3-многообразия есть конечное покрытие, расслаивающееся по кругу, то есть, построенное склеиванием противоположных частей утолщенной поверхности. Из ВГХ мы знаем, что у многообразия есть конечное Хакеново покрытие – то есть, в покрытии есть встроенная несжимаемая поверхность. Если вскрыть многообразие Хакена вдоль этой поверхности, вы получите нечто, что выглядит, как утолщённая поверхность на концах, но как бог знает что в «кишках».

Ян Эйгол во время недавнего путешествия в Тэджон, Южная Корея

В 2008 произошёл, по словам Калегари, «удивительный прорыв», когда Эйгол показал, что гиперболические 3-многобразия, удовлетворяющие особым техническим условиям, гарантировано виртуально расслаиваемы. В следующем году Вайз на этой основе показал, что все многообразия Хакена виртуально расслаиваемы. То есть, существует способ развернуть многообразие Хакена, чтобы получить конечное покрытие, раскрывающее сложную топологию и приводящее к простому расслоённому многообразию. Поэтому, если многообразие будет виртуально Хакеновым, оно должно быть виртуально расслаиваемым.

«Думаю, все верили, что ВГХ окажется верной, но гипотеза виртуального расслоения казалась нам менее доступной,– сказал Калегари. – По мне, тот факт, что гипотеза виртуального расслоения следует из ВГХ, является одной из самых шокирующих сторон всей этой истории».

С доказательством гипотезы виртуального расслоения

«вы можете поддаться искушению и решить, что 3-многообразия слишком просты, поскольку многообразия, расслаивающиеся по кругу, просты,– сказал Мински. – Но я думаю, что это учит нас, что многообразия, расслаивающиеся по кругу, совсем не просты, и более хитрые, чем мы ожидали».

В то же время теорема виртуального расслоения значит, что существует простой и информативный рецепт создания всех компактных гиперболических 3-многообразий: начните с утолщённой поверхности, склейте вместе её внутреннюю и внешнюю границу с поворотами по вашему вкусу, и сложите многообразие на себя конечное количество раз.

«Если бы вы попросили у меня гиперболическое 3-многообразие, я бы спросил, какой тип вам нужен – какой тип расслоения и конечного покрытия? – говорит Калегари. – Теперь мы знаем, что в этом процессе мы не пропускаем ни одно 3-многообразие».

И хотя математикам потребуется время на тщательную проверку работы Эйгола, многие из них оптимистично считают, что проверку она пройдёт.

«Ян Эйгол не небрежный человек»,– говорит Мински.

Теперь, когда, по-видимому, последний вопрос из списка Тёрстона разрешён, исследователи начинают задаваться вопросом, как будет выглядеть область топологии 3-многообразий в дивном новом мире после Тёрстона.

Математики соглашаются, что у них будет много работы с поиском полезных вещей, которые смогут предложить КК для поддающихся кубированию форм. А для самих 3-многообразий, по словам Эйгола, наступил конец эпохи – и начало следующей.

«В большинстве областей математики нет плана, который мог бы обрисовать путь на 20–30 лет вперёд, как это было у нас»,– говорит он. Теперь, предполагает он, топология 3-многообразий и геометрия могут стать похожими на другие области математики, в которых учёные идут на ощупь и достигают прогресса даже без такой роскоши, как большая гипотетическая картина происходящего.

«Новые поколения математиков придумают следующие важные вопросы»,– говорит Эйгол.