Совсем недавно японские и итальянские математики рассказали орешении важной задачи из теории минимальных поверхностей — о поведении мыльной пленки на гибком каркасе. Как часто бывает в физике, эта теоретическая задача связана с гораздо более широким кругом явлений, чем простое возникновение мыльных пленок: от динамики молекул до гравитационных полей черных дыр. Мы предлагаем вам небольшой экскурс в одну из самых красивых задач математики — задачу Плато о минимальных поверхностях.

Историю этой задачи следует начать с работ бельгийского физика Жозефа Плато, кстати, изобретателя стробоскопа. В первой половине XIX века ученый занимался исследованием геометрии мыльных пузырей и сложных конструкций из мыльных пленок. Бельгиец пытался описать закономерности, которые возникают в мыльной пене, и сформулировал несколько законов, известных как «законы Плато». Например, оказалось, что средняя кривизна поверхности мыльной пленки одинакова во всех ее точках.

Мыльные пленки были выбраны ученым не случайно. Как известно, любая физическая система стремится минимизировать свою энергию. Шар, находящийся на склоне горы, покатится вниз, так как стремится уменьшить потенциальную энергию, электрический конденсатор постепенно разрядится и так далее. Точно так же и мыльная пленка попытается уменьшить свою энергию, если это возможно. Так как эта энергия запасается в поверхностном натяжении (чем больше площадь поверхности, тем больше ее энергия), то пленка стремится обладать геометрией с минимальной площадью поверхности, оптимизируя любые изгибы и стыки.

Это приводит на практике к необычным закономерностям. Например, оказалось, что в мыльной пене пленки «стыкуются» друг с другом строго тройками, под углом 120 градусов. На пересечении таких плоскостей формируются так называемые «границы Плато». Они, кстати, тоже пересекаются между собой — только четверками, под углом равным 109,5 градуса (это угол, под которым из центра тетраэдра видны его вершины). Как отметил Плато, любые другие конфигурации в мыльной пене неустойчивы.

Владимир Королёв

На самом деле проблема минимальной поверхности была сформулирована почти за век до экспериментов Плато французским математиком Жозефом-Луи Лагранжем. Ученый, создавший теорию вариационного исчисления, задался вопросом, как минимизировать площадь поверхности, заключенной в данном трехмерном контуре. Можно показать математически, что минимальные поверхности обладают определенным свойством: их средняя кривизна поверхности равна нулю.

Оригинальная задача была поставлена в 1760-х годах. Вопрос, который поставил Лагранж, формулировался так: всегда ли можно построить минимальную поверхность для заданного контура? С точки зрения математики, у этой задачи есть около десятка эквивалентных формулировок, одна из которых требует доказать существование решения дифференциального уравнения второго порядка для заданных граничных условий (трехмерного каркаса).

Очевидный способ доказать существование такой поверхности — найти прямое решение уравнения для всех возможных каркасов, то есть указать метод построения минимальной поверхности. Однако в математике есть и еще один способ доказательства таких утверждений — так называемые «чистые доказательства существования». Например, можно доказать, что у многочлена нечетной степени всегда есть хотя бы один действительный корень. Это непрерывная функция, которая при больших положительных «иксах» будет положительной, а на больших отрицательных «исках» — отрицательной (или наоборот). Это означает, что в какой-то момент она должна будет пересечь ось абсцисс — эта точка и будет искомым корнем. Но при этом такое доказательство не указывает на способ поиска этого корня.

Жозеф Плато подошел к этой задаче с «другого конца», показав, как построить физически минимальную поверхность для заданного замкнутого контура. Для этого достаточно просто сделать этот каркас из проволоки и окунуть его в мыльный раствор. Но, разумеется, доказательством существования минимальных поверхностей работы физика послужить не могли. Зато в честь его работ вопрос, сформулированный Лагранжем, стал известен как «задача Плато». Интересно, что правила, которые сформулировал бельгиец, оказались верны для всех минимальных поверхностей. Это было подтверждено в 1970-х годах с помощью геометрической теории меры.

На доказательство существования минимальных поверхностей ушло почти 200 лет. Математики находили решения для отдельных частных случаев (например, когда каркас состоит из прямолинейных отрезков), но доказать утверждение в наиболее общем виде удалось лишь в 1930 году. Этот результат независимо друг от друга получили Джесси Дуглас и Тибор Радо. За свое оригинальное решение в 1936 году Дуглас получил первую в истории Филдсовскую премию.

Построение минимальных поверхностей — отдельная проблема, которая тоже была решена. Для этого были разработаны специальные методы, о ряде которых можно прочитать в брошюре Алексея Сосинского. Например, необычно выглядит способ построения минимальной поверхности с помощью случайных блужданий. Он устроен следующим образом. На первом этапе спроецируем каркас на лист бумаги в клеточку (посмотрим на его тень). Пусть линии на листе бумаги — улицы города, тень каркаса – его граница. Поместим в узел клетки пьяницу — объект, который случайным образом будет поворачивать на каждом перекрестке. Когда пьяница пересекает границу города, он падает в канаву и его штрафует полицейский. Сумма штрафа зависит от высоты точки каркаса, отбрасывающей тень на конкретную «канаву».

Оказывается, средняя величина штрафа для каждой отправной точки пьяницы численно равна высоте минимальной поверхности, натянутой на данный каркас. Этот метод относится к классу методов Монте-Карло.

После работы Дугласа задачу Плато начали обобщать. К примеру, в четырехмерном пространстве можно ввести трехмерные «поверхности» и так далее. Задача о существование таких минимальных суперповерхностей была решена российским математиком Анатолием Фоменко. Во второй половине XX века математики рассмотрели вариант задачи о мыльных пленках на гибких каркасах и даже решили его для частных случаев. В 2017 году вышла публикация с решением наиболее реалистичной формулировкой этой задачи — с гибким каркасом конечной толщины.

Есть у истории с минимальными поверхностями еще один интересный поворот. Более 200 лет считалось, что существуют всего три класса таких объектов: плоскости, катеноиды и геликоиды — если не рассматривать пересекающиеся поверхности. Катеноиды возникают, когда пленка оказывается натянутой между двумя параллельными кольцами. Геликоиды — спиральные ленты, появляющиеся на соответствующих спиральных каркасах.

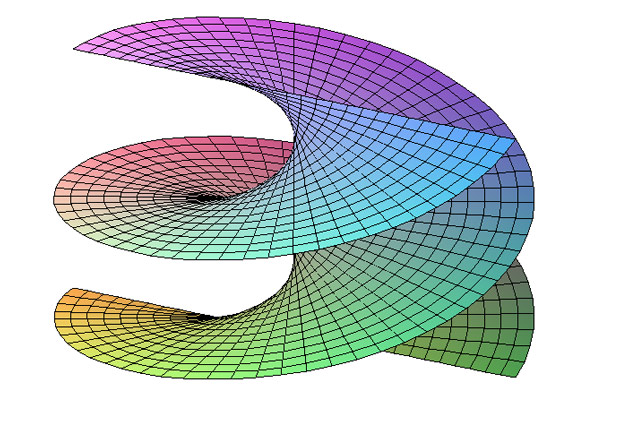Геликоид. Jens Dittrich / CC-BY-SA-3.0

Катеноид. Jens Dittrich / CC-BY-SA-3.0

В 1978 году бразильский математик Хосе де Коста обнаружил новый пример минимальной поверхности, не эквивалентный трем предыдущим. Эта фигура, натянутая на три проволочных кольца, была изоморфна тору с тремя отверстиями (непрерывной деформацией ее можно превратить в тор с тремя ручками). Это неожиданное открытие стало важным импульсом, который позволил открыть бесконечно большой класс «дырявых» минимальных поверхностей.

Anders Sandberg / CC BY-SA 3.0

Задача может показаться малоприменимой — в самом деле, моделирование мыльных пленок не выглядит важной проблемой современной науки. Однако уравнения, описывающие минимальные поверхности, возникают и в других областях физики, а сами поверхности, ввиду своих особенных свойств, используются в моделировании новых материалов.

К примеру, существуют периодические минимальные поверхности: они состоят из повторяющихся элементов с минимально возможной площадью. Особенно примечательны гироиды — бесконечные, трижды периодические структуры (с периодичностью вдоль трех осей). Такие поверхности были обнаружены в природе, например в мембранах хлоропластов, а также в кутикулярных образованиях на крыльях бабочек.

Гироид

Гироид также интересен как геометрический структурный мотив, гарантирующий минимальную плотность для пористого материала заданной периодичности. Это предположение использовалось инженерами из MIT при попытке оценить, можно ли создать трехмерный материал легче воздуха и достаточно прочный, чтобы он мог выдержать атмосферное давление. В основу гироидного материала физики заложили графен, но, к сожалению, надежды ученых не оправдались.

Минимальные поверхности пригодились и самим математикам. Оказывается, если попытаться описать броуновское (хаотичное) движение на минимальных поверхностях, то с его помощью можно доказать теоремы Лиувилля вероятностными методами.

Но самым необычным случаем, в котором сыграла важную роль задача Плато, стало описание горизонтов событий черных дыр. С точки зрения геометрии, наш мир можно описать как четырехмерное пространство (пространство Минковского), в котором три координаты устроены так же, как и в обычном евклидовом пространстве, а четвертая — временная.

В таком пространстве тела могут перемещаться только по определенным траекториям (это связанно с тем, что ничто не может двигаться быстрее скорости света). В окрестностях черной дыры в таком пространстве возникает особенность — поверхность горизонта событий. Оказывается, что уравнения, которыми задается кажущийся горизонт событий в условиях симметричного времени, совпадают с уравнениями минимальных поверхностей. Иными словами, горизонты событий, по сути, представляют собой минимальные поверхности.

Аппарат для исследования минимальных поверхностей был использован китайским математиком Яу Шинтаном для доказательства теоремы о положительности энергии. Она утверждает, что средняя энергия Вселенной (как изолированной системы) неотрицательна. Этот факт чрезвычайно важен для общей теории относительности: пространственно-временной континуум может быть стабилен только в случае, если эта теорема верна. Подробнее об этом факте можно прочесть в книге Яу «Теория струн и скрытые измерения Вселенной». Кстати, позднее Яу описал специальный класс многообразий (поверхностей), играющий ключевую роль в современной теории струн.

Задача о минимальных поверхностях — лишь один пример из большого цикла классических задач вариационной геометрии. Исторически первой вариационной задачей считается задача Дидоны, связанная с легендой об основании Карфагена: «Какую наибольшую площадь можно окружить кривой заданной длины?». Есть среди них и еще одна задача о мыльных пленках, точнее, о мыльных пузырях. «Верно ли, что наименьшее по площади поверхности тело, ограничивающее два заданных объема — это двойной мыльный пузырь?». Она продержалась дольше, чем классическая задача Плато — полное доказательство задачи о двойном пузыре было опубликовано всего 15 лет назад. Кстати, ей в свое время тоже занимался Жозеф Плато.

Автор: Владимир Королёв