Свет — это и волна, и частица, которая движется сквозь пространство с максимально возможной для нашего мира скоростью. Скорее всего, свет не имеет массы. Попробуйте себе представить зрительный образ такого объекта, и почти наверняка вы будете мыслить о чем-то эфемерном и бестелесном, к чему невозможно прикоснуться и что не «поймать». Однако живая природа и, в частности, человечество сумели приспособить эту капризную сущность для своего удобства, а ученые открывают все новые и новые свойства световых волн, или фотонов. Недавно их даже научились сжимать. И это новое умение стало толчком к другому, более известному открытию — недавнему экспериментальному детектированию гравитационных волн. Что имеют ввиду ученые, когда говорят о сжатых состояния света? И почему без них было бы невозможно «увидеть» гравитационные волны? На эти и некоторые другие вопросы мы попробуем ответить в нашем тексте.

Что такое «сжатые состояния света»?

Начнем с того, что Джеймс Максвелл сопоставил понятие света и электромагнитной волны, существование которой было предсказано в его теории. Эта волна имеет, как можно догадаться, две составляющие — электрическую и магнитную. Каждая из них — это периодическое колебание некой величины, которая характеризует то или иное поле. Для электрического поля это напряженность (Е), для магнитного — индукция (В).

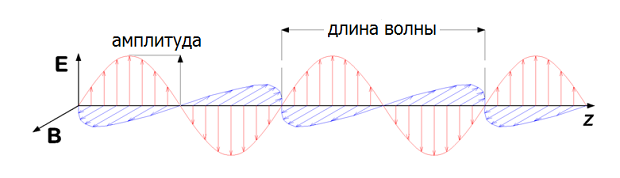Иллюстрация классической электромагнитной волны. Фазовый сдвиг (по оси z) в данном случае отсутствует. Wikimedia Commons

В простейшем случае при движении волны концы векторов напряженности и индукции описывают синусоиды в плоскостях, расположенные под углом в 90 градусов. Такой свет называют линейно-поляризованным. «Линейно», потому что если «смотреть» на вектор, например, напряженности, находясь на линии пересечения вышеупомянутых плоскостей, то будет казаться, что он просто колеблется на одной линии, например, вправо-влево. Но если посмотреть на эти колебания из другой точки, расположенной не в плоскости колебания, то станет «видно», что концы векторов описывают синусоиды (или косинусоиды, кому как удобнее). Максимумы синусоиды (вершина горба) определяют амплитуду волны, расстояние между соседними горбами — длину волны, а сдвиг вдоль направления ее распространения — фазу. Для объяснения термина «сжатый свет» в случае волны с линейной поляризацией будет достаточно даже одной синусоиды, например, вектора напряженности.

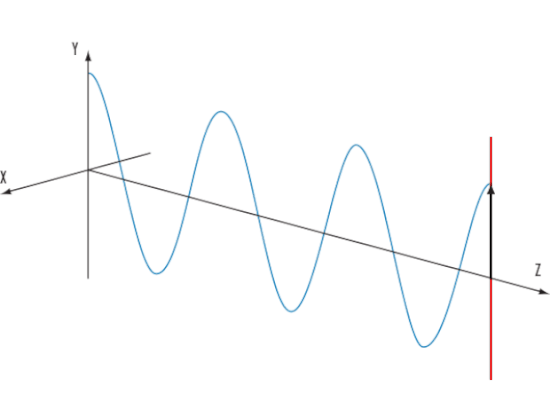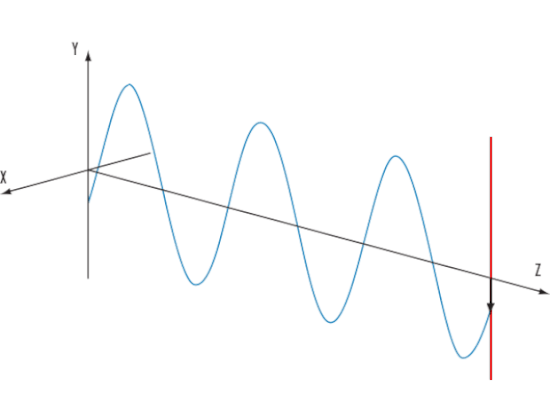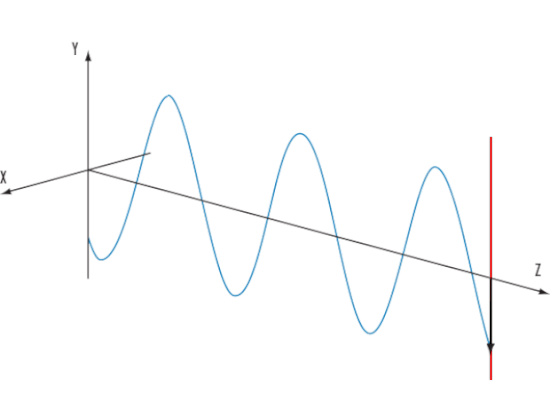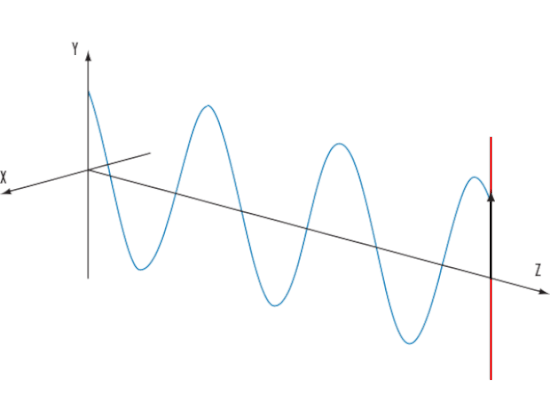Пример волны с линейной поляризацией. В данном случае вектор поляризации испытывает колебания вдоль направления Y (черная движущаяся стрелка). Wikimedia Commons

Для дальнейших рассуждений нам потребуется уже квантовая физика. Для начала сравним один из аспектов, который различается при рассмотрении света как электромагнитной волны в классической и квантовой физике. А именно причины возникновения шумов, или неопределенностей для амплитуды и фазы волны.

Представьте, что вы рисуете синусоиду для электрической напряженности световой волны в пространстве с помощью некоего магического карандаша. Если карандаш «классический», его кончик может быть бесконечно тонким, следовательно, такой же бесконечно тонкой будет и линия синусоиды. Но для многих применений нас интересует когерентное, то есть согласованное излучение, например, совпадающее по фазе. Также будем считать, что мы имеем дело с идеальным монохроматическим излучением, то есть вариаций длины волны нет. Тогда вы должны нарисовать еще много таких синусоид, совпадающих с первой. При этом результирующая кривая, представляющая собой определенным образом составленную сумму всех синусоид, также будет бесконечно тонкой.

Однако если оборудование, с помощью которого вы создаете волну, неточное или среда распространения света неоднородная, синусоиды будут немного сдвинуты друг относительно друга и амплитуда излучения может различаться со временем. Представьте теперь, что вы находитесь в некоей точке на пути электромагнитной волны и рисуете развертку приходящего сигнала напряженности электрического поля от времени. Из-за неточностей, вносимых аппаратурой, амплитуда и фаза волны в эквивалентных точках (удаленных друг от друга на длину волны), будут немного различаться. Повторите такой эксперимент много раз, накладывая каждый последующий рисунок на предыдущий (начинать следует с эквивалентной точки). Через достаточное количество повторений вы увидите, что первоначальная кривая размылась и приобрела конечную толщину. Такой когерентный свет является «шумным», или, другими словами, он имеет неопределенность по амплитуде и фазе.

Теперь представим идеализированную ситуацию, в которой вы смогли избавиться от всех шумов, связанных с оборудованием или средой. Тогда, если вы хотите нарисовать результирующую кривую напряженности, пользуясь классическим представлением света, ничто не может запретить вам использовать бесконечно тонкий карандаш. И вот здесь возникает расхождение с представлением квантовым, поскольку «квантовый» карандаш всегда имеет конечную толщину. Определяется эта толщина соотношением неопределенностей Гейзенберга — фундаментальным соображением, согласно которому некоторые пары наблюдаемых величин не могут быть одновременно измерены со сколь угодно большой точностью. Такими парами являются импульс и координата частицы, энергия и временная координата, амплитуда и фаза электромагнитной волны.

В квантовой электродинамике причину «шумности» «квантового света» обычно объясняют следующим образом. Из-за соотношения неопределенностей Гейзенберга (для пары энергия-время) вакуум — это вовсе не пустое пространство. Энергия вакуума варьируется со временем, и эти колебания энергии можно представить как рождение и исчезновение пар неких виртуальных частиц. Несмотря на то, что энергия и время жизни этих частиц (их еще называют квантовыми флуктуациями вакуума) очень мала, они могут успеть провзаимодействовать со световой волной, которую мы с таким старанием «рисовали». В результате этого взаимодействия параметры волны немного изменяются, и это становится причиной «квантового шума», который определяет конечную толщину «квантового» карандаша.

Итак, мы наконец-то подобрались вплотную к тому, чтобы дать определение «сжатым состояниям света». Мы выяснили, что свойства вакуума таковы, что в нем всегда присутствуют «шумы», которые заставляют нас «рисовать» световую волну как будто плохо заточенным карандашом, внося неопределенность в ее фазу и амплитуду. При этом очевидно, что величины, входящие в соотношение неопределенностей (амплитуда и фаза) равноправны. Поэтому толщина линии, в виде которой мы договорились представлять электромагнитную волну, одинакова на всем протяжении распространения волны. В случае же сжатого света это не так. Линию для сжатого состояния света необходимо рисовать карандашом конечной толщины неравномерным его нажатием. Таким образом, в каких-то ее областях толщина будет меньше некой стандартной (сжатое состояние), зато это будет компенсироваться увеличенной толщиной в других (назовем их раздутыми состояниями).

а) Зависимость напряженности от времени для несжатого когерентного состояния света (слева) и иллюстрация изотропного «квантового шума» (справа); Carlton M. Caves / Physical Review D, 1982

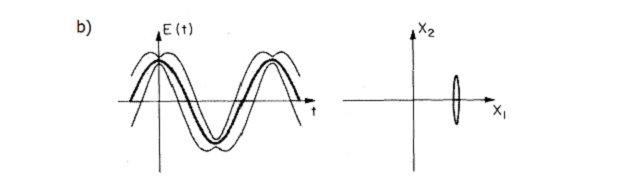b) Зависимость напряженности от времени для света, сжатого по амплитуде (слева), и иллюстрация неизотропного «квантового шума» (справа) для этого состояния; Carlton M. Caves / Physical Review D, 1982

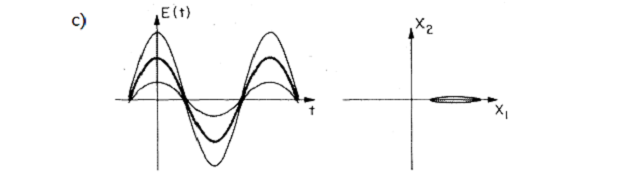b) Зависимость напряженности от времени для света, сжатого по фазе (слева), и иллюстрация неизотропного «квантового шума» (справа) для этого состояния; Carlton M. Caves / Physical Review D, 1982

Помимо вариаций толщины линии, есть еще одна иллюстрация сжатых состояний света. Можно «рисовать» не саму волну, а только ее неопределенность, или «квантовый шум» для двух величин, которые входят в соотношение неопределенностей. Тогда для некоего когерентного состояния (в том числе с нулевым числом фотонов, то есть для вакуума) диаграмма шума будет представлять собой круг, а окружность, которая его ограничивает — уровень «шума». В случае сжатого света это будет не круг, а эллипс той же или большей площади. Таким образом, может получиться, что в некоторой области (рядом с меньшим диаметром эллипса) сжатый свет будет гораздо менее «шумным», чем вакуум, где нет никаких световых волн!

Говоря о фотонах, следует обратить внимание, что во всех наших рассуждениях, которые касаются квантовой природы света, нужно учитывать, что свет — это не просто волна, а еще и частица-фотон. Например,сжатый вакуум представляет собой не просто волну с нулевой средней амплитудой, а еще и пучки четного числа фотонов. Чтобы не усложнять и без того громоздкие объяснения, в данном тексте мы часто упускали это из виду, продолжая рассуждать в рамках только волновой теории. Разумеется, мы упускали и множество других особенностей квантового описания света, оставляя только те факты, которые нам показались необходимы при объяснении термина «сжатые состояния света».

Зачем нужно сжимать свет?

Одно из самых известных и при этом успешных применений сжатых состояний света — в эксперименте по обнаружению гравитационных волн, предсказанных Эйнштейном еще в 1916 году. Первая в истории волна пространства-времени, которую удалось зафиксировать человечеству, прошла через Землю 14 сентября, вторая — 26 декабря 2015 года. И только в феврале 2016-го, через 100 лет после теоретического предсказания, научное сообщество окончательно заявило об открытии этого уникального явления (больше о гравитационных волнах можно прочесть в материале «На гребне метрического тензора»).

Почему же ученым потребовалось так много времени? Все дело в том, что гравитационные волны очень слабые. Потребовалось целых 100 лет для того, что наука и техника развились настолько, чтобы достичь нужной точности. Но, как мы уже выяснили, в квантовой физике для достижения идеальной точности есть фундаментальный запрет — неопределенность Гейзенберга — и тесно связанный с ним стандартный квантовый предел. Последний представляет собой «неопределенность Гейзенберга» не для пары, а для какой-то конкретной величины при ее многократном измерении. Квантовые пределы «работают» не для всех величин, а только для некоторых. (Физики говорят, что стандартный квантовый предел накладывается на величины, оператор которых не коммутирует сам с собой. Неопределенность Гейзенберга «работает» в случае, если операторы двух величин не коммутируют друг с другом.) Но по иронии судьбы работа детектора LIGO — самой точной в инструментальном смысле установки по регистрации гравитационных волн — оказалась основана на явлении интерференции, точность которого ограничена квантовым пределом.

В этой установке два луча проходят через четырехкилометровые туннели и встречаются на светоделителе (таком, как полупрозрачное зеркало), после чего с помощью системы детекторов ученые ищут любые крошечные изменения интерференционной картины. Эти изменения могут возникнуть, если расстояния, которые проходит свет в туннелях, меняются: свет проходит разный путь, и фазы волн, приходящих на детектор, рассинхронизируются, а значит, меняется интерференционная картина. Если устранить все возможные «дрожания» установки, вызванные сейсмическими толчками, шумом ближайшей автострады или даже чиханием сотрудника коллаборации LIGO, то станет возможным зафиксировать дрожания самого пространства-времени — гравитационные волны.

Но оказалось, что и этого недостаточно. Даже такие грандиозные события, как слияния двух черных дыр, в большинстве случаев будут давать сигнал, сравнимый по величине с «квантовым шумом». Поскольку подобные события сами по себе довольно редки во Вселенной, то вероятность увидеть достаточно сильные гравитационные волны, какие смогла бы зафиксировать установка с «квантовым уровнем точности», еще меньше. Пройдут десятилетия, Земля испытает на себе действие сотен гравитационных волн, но все они останутся невидимы для ученых, поскольку их сигнал будет сравним с уровнем «квантовых шумов».

Вот тогда ученым и потребовался сжатый свет. А точнее даже сжатый вакуум. Под вакуумом в данном случае понимается состояние электромагнитной волны, в котором амплитуда его колебаний в среднем равна нулю (вспомните, что она при этом может отклоняться от нуля как раз за счет «шумовых флуктуаций»). Грубо говоря, ученые берут две одинаковые электромагнитные волны и накладывают их друг на друга таким образом, чтобы они погасили колебания друг друга. Если положение минимума синусоиды одной волны совпадет с максимумом другой волны, то суммарно они дадут ноль. Однако если еще хоть немножко сместить волны друг относительно друга (сдвинуть по фазе), то сразу станет понятно, что в этом так называемом «вакууме», вообще-то, есть фотоны. А что если эти фотоны еще и предварительно сжать? 

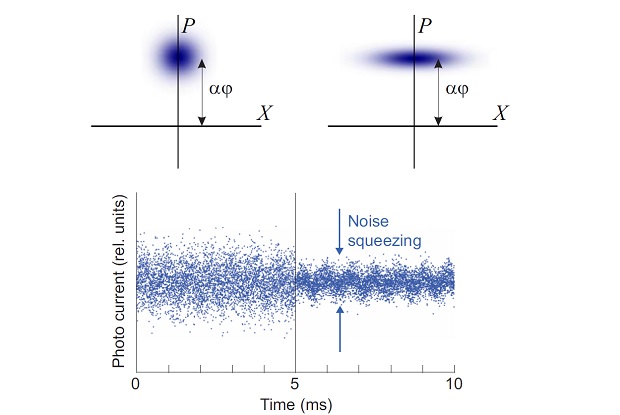Иллюстрация состояния вакуума, сжатого по фазе (вверху справа), в сравнении с обычным вакуумным состоянием (вверху слева). На нижнем рисунке показано, как использование сжатого вакуума помогает снизить уровень «шума» для сигнала, измеряемого интерферометром (симуляция). Roman Schnabel et. al/ Nature Communications, 2010

Именно это странное ничто — состояние света, называемое сжатый вакуум, — ученые и пускают путешествовать по многокилометровым тоннелям LIGO и другим частям установки. С одной стороны, фотонов в нем «не видно», средняя амплитуда электромагнитных колебаний равна нулю. С другой стороны, все остальные свойства распространяющейся волны сохраняются. Например, если квантовый шум для какой-то компоненты был сжат в первичной волне, то и в «вакуумной» волне он останется сжатым. Сжатое состояние взаимодействует в тоннелях с лазерными лучами, которые детектируют гравитационные волны, и тем самым в разы повышает точность установки. Забавно, что именно достижение переднего края квантовой физики позволило подтвердить гениальное предсказание в области теории гравитации, с которой эту самую квантовую физику никак не удается состыковать (речь идет о попытках создания Теории Всего).

Схема установки для сжатия света. ANU

Создание сжатых состояний света стало возможным благодаря развитию экспериментальной нелинейной оптики. Этот раздел физики изучает различные явления, которые возникают при взаимодействии света большой интенсивности с веществом. Грубо говоря, для создания сжатых состояний света ученым из LIGO потребовался первичный луч высокой интенсивности, резонатор и особый кристалл, который позволяет луч одной частоты (или энергии) разбивать на два луча с меньшей частотой. Такая система называется оптический параметрический осциллятор (англ. термин — Optical parametric oscillator, или OPO) и позволяет генерировать состояния света или «вакуума» с уменьшенным значением «квантового шума» по заранее выбранной компоненте, например, фазе волны. Существуют и другие способы создания сжатых состояний света, однако они также основаны на других различных эффектах из нелинейной оптики.

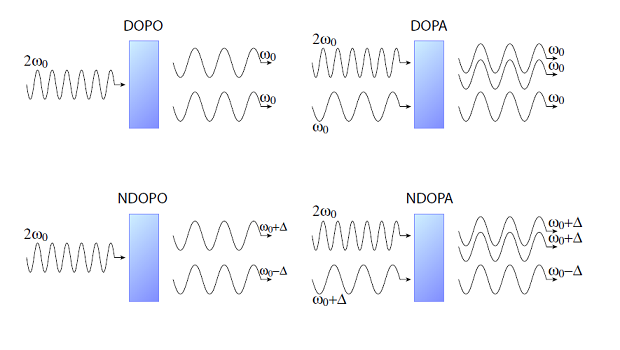Нелинейные эффекты, которые используются для создания сжатых состояний света (optical parametric oscillation (OPO) и amplification OPA). Обозначения D и ND показывают, образуются ли фотоны одинаковой энергии (degenerate) или разной (non-degenerate). Simon Chelkowski / PhD Thesis, Hannover, 2007

Одна из первых установок по созданию сжатого света, использующая нелинейный эффект OPA: a) схема установки; b) нелинейный кристалл MgO:LiNbO₃; с) и d) устройство и внешний вид оптического резонатора. Roman Schnabel et. al / Nature Communications, 2010

Схема устройства для получения сжатого вакуума, используемая в установке по регистрации гравитационных волн LIGO. Сжатый вакуум генерируется в резонаторе, работающем на эффекте OPO, а затем попадает в саму установку-интерферометр. The LIGO Scientific Collaboration / Nature Photonics, 2013

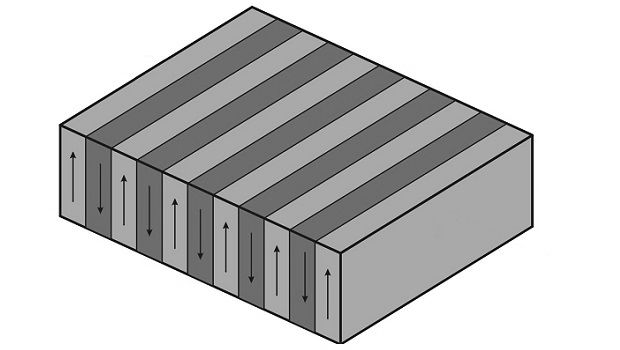В качестве нелинейного кристалла в установке LIGO используется титанил фосфат калия KTiOPO₄ с регулярной доменной структурой, которая представлена на рисунке. Стрелками показано направление вектора поляризации в кристалле. Екатерина Митрофанова

В заключение следует отметить, что сжатые состояния существуют не только для света, но и для других квантовых объектов. Например, можно создать облако переохлажденных атомов из рубидия, «сжатых по спину», и такие системы ученые планируют использовать в качестве сверхточных атомных часов. Идея остается той же — уменьшая шумы для компоненты спина вдоль одной оси, шумы для направлений спина вдоль других осей увеличиваются. Таким образом, соотношение неопределенностей Гейзенберга оказывается ненарушенным, никакие физические законы квантовой теории не опровергаются. Но все же сжатые состояния позволяют ученым в последнее время достичь беспрецедентной точности физических измерений. Даже сам создатель теории относительности Альберт Эйнштейн полагал такую точность практически невозможной, считая, что именно по этой причине гравитационные волны так никогда и не удастся наблюдать в эксперименте. Впрочем, говорят, и в квантовую механику он тоже поначалу не верил.

Автор: Екатерина Митрофанова