Автор: Дионис Диметор. «Но если квантовая механика — это не физика в обычном смысле, если она не занимается ни веществом, ни энергией, ни волнами, ни частицами, то чем же она занимается? С моей точки зрения, она занимается информацией, вероятностями, наблюдаемыми величинами и тем, как они соотносятся друг с другом» (Скотт Ааронсон).

«Исторически сложилось так, что большая часть фундаментальной физики была связана с открытием фундаментальных частиц природы и уравнений, описывающих их движение и взаимодействие. Теперь кажется, что другая программа может быть не менее важной: обнаружить способы, которыми природа допускает и предотвращает проявление информации и манипулирование ею». (Эндрю Стин, «Квантовые вычисления»).

Когда речь заходит о законах сохранения, первым на ум приходит закон сохранения энергии. Менее известны законы сохранения заряда, импульса, момента импульса и чётности. Но что такое закон сохранения информации, зачастую не могут понятно объяснить даже сами физики. О нём мало пишут в научно-популярной литературе, потому что тема запутанная и нагружена математикой. А потом популяризаторов заводят в тупик, когда спрашивают, почему информация должна сохранятся в чёрных дырах или при квантовом измерении. Рассказать об этом не на математическом, а на естественном языке практически невозможно, но я всё же попробую, используя понятийный аппарат квантовой механики и аналогии с классической информацией. Мы выясним, что такое квантовая информация, сохраняется ли она при любых операциях с частицами, или есть исключения, которые приводят к потере информации, и как это связано с фундаментальной симметрией физических процессов.

Теорема Нётер и CPT-инвариантность

Для начала расскажем о понятии симметрии в физике и о вкладе в науку Эмми Нётер, которую Альберт Эйнштейн назвал «самым значительным творческим гением математики, появившимся с тех пор, как женщинам позволили получать высшее образование».

Эмми Нётер (1882–1935)

Одним из важнейших понятий в физике является инвариантность – неизменность физической величины по отношению к некоторым преобразованиям, например, во времени и пространстве, и при переходе от одной системы отсчёта к другой. Это означает, что, какие бы мы не проводили операции (преобразования) с материей, на выходе должны получиться те же значения, которые были на входе. Учитывая, что пространство и время однородны (имеют одинаковые свойства во всех точках или моментах) и изотропны (имеют одинаковые свойства по всем направлениям), все физические процессы должны быть симметричными. Симметрия означает сохранение какой-то характеристики при изменениях (преобразованиях). Симметричным называют объект, который можно как-то изменять, получая в результате объект, совпадающий с первоначальным.

В соответствии с доказанной в 1915 г. теоремой Нётер, если система обладает непрерывной симметрией, то существуют соответствующие величины, значения которых сохраняются во времени. Каждой непрерывной симметрии физической системы соответствует свой закон сохранения:

• Однородности времени – закон сохранения энергии;
• Однородности пространства – закон сохранения импульса;
• Изотропии времени – закон сохранения чётности;
• Изотропии пространства – закон сохранения момента импульса;
• Калибровочной симметрии – закон сохранения электрического заряда.

Самый известный из списка – закон сохранения энергии, который гласит, что полная энергия замкнутой системы остаётся постоянной, что бы с этой системой не происходило. Поскольку энергия и масса эквивалентны (E=mc2), ничто не может возникнуть из ниоткуда и исчезнуть в никуда. Если столкнуть два протона, то суммарная масса образовавшихся частиц и выделившаяся в результате реакции энергия будут в точности равны массе и кинетической энергии двух исходных частиц. Если у каждого из этих протонов был заряд +1, то у частиц на выходе суммарный заряд будет +2 – это закон сохранения заряда. Если частица движется в определённом направлении, она не может самопроизвольно изменить траекторию, пока с чем-нибудь не столкнётся – это закон сохранения импульса. То же самое с вращением: если что-то крутится по часовой стрелке, оно не может само остановиться и начать вращаться против часовой стрелки – это закон сохранения момента импульса. Ну и закон сохранения чётности требует зеркальной симметрии физических процессов, то есть эквивалентности правого и левого.

В списке Нётер отсутствует, но неявно подразумевается ещё один, самый главный закон – закон сохранения информации. Из него математически выводятся все остальные законы сохранения. С точки зрения квантовой механики, симметрия физической системы – это преобразование, которое переводит одни решения уравнения эволюции в другие решения того же уравнения. Если где-то симметрия нарушается, значит, мы упустили какую-то часть уравнения. В 1927 г. сохранение чётности было возведено Юджином Вигнером в ранг универсального закона природы, но с тех пор этот закон нарушался уже дважды. В 1956 г. группой Ву Цзяньсюн было обнаружено нарушение пространственной чётности (P-инвариантности) в слабых взаимодействиях (при бета-распаде), и Лев Ландау в 1957 г. предложил ввести СР-инвариантность (Charge-Parity – заряд-чётность), то есть комбинированную симметрию зарядового сопряжения и зеркального отражения. С-инвариантность предполагает симметрию материи и антиматерии: частицы и античастицы имеют одинаковые числовые значения массы, заряда и спина, только заряд у них противоположен по знаку, а спин – по направлению. В 1964 г. Джеймс Кронин и Вэл Фитч доказали, что в слабых взаимодействиях может нарушаться даже СР-симметрия: некоторые реакции распада мезонов проходят вперёд во времени быстрее, чем назад. Некоторые специалисты увидели в этом причину необратимости времени, но сейчас мало кто всерьёз думает, что столь незначительные эффекты могут лежать в основе второго закона термодинамики.

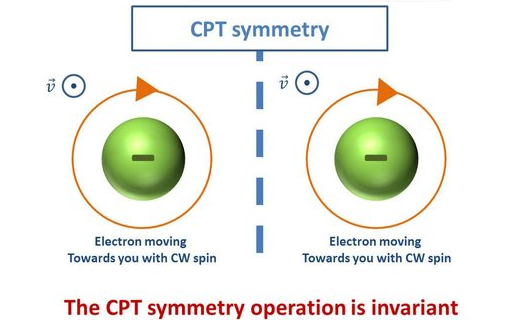
В итоге физики остановились на СРТ-инвариантности (Charge-Parity-Time – заряд-чётность-время), которая следует из доказанной в 1954 г. теоремы Людерса-Паули. Инвариантность относительно обращения времени (T-симметрия) означает, что если движение разрешено законами физики, то обратное движение тоже разрешено. Согласно теореме Людерса-Паули, если поменять всю материю нашей Вселенной на антиматерию, зеркально отразить импульсы и положения всех частиц и обратить время вспять – полученная антивселенная будет вести себя точно так же, как и наша Вселенная. Время в такой антивселенной будет идти назад, заряды всех частиц будут противоположными, а лево и право или одно из двух других измерений поменяются местами. CPT-инвариантность считается одним из наиболее фундаментальных принципов функционирования вселенной, наряду с постоянством скорости света в вакууме. На ней держится квантовая теория поля – самая точная и экспериментально подтверждённая физическая теория.

Квантовая информация

Что такое квантовая информация и чем она отличается от классической? Начнём с простого. Основная идея квантовой физики заключается в том, что фундаментальными составляющими материи являются кванты, они же – элементарные частицы, они же – колебания квантовых полей. У частиц есть свои степени свободы – постоянные и переменные параметры, или наблюдаемые величины – величины, которые мы можем в принципе измерить в ходе эксперимента. Постоянными являются такие параметры, как масса покоя, заряд, значение спина, «цвет», «аромат» и т.д., а переменными – координата, скорость/импульс, энергия, частота/длина волны, поляризация, направление спина, квантовые числа электрона в атоме и т.д. Постоянные параметры одинаковы у всех частиц одного типа (фотон, электрон, нейтрино, кварки и т.д.) и прописаны в Стандартной модели. Они нас сейчас вообще не интересуют: будем во всех примерах использовать электрон, который имеет массу 0,5 МэВ, заряд –1 и спин 1/2. Переменные параметры, разумеется, могут отличаться. Николя Жизан в книге «Квантовая случайность» сравнивает постоянные и переменные параметры частицы с философскими понятиями содержания и формы:

«Аристотель говорил о двух существенных ингредиентах – о содержании и о форме. Сегодня физики говорят о веществе и о физическом состоянии. К примеру, письмо сделано из бумаги и чернил, что являет собой вещество, и содержит текст, то есть информацию, или физическое состояние бумаги и чернил. Для электрона вещественное — это его масса и электрический заряд (наряду с другими постоянными характеристиками), в то время как облака потенциальных координат и скоростей формируют его физическое состояние. Для фотона — безмассовой частицы света — вещественной является его энергия, а физическое состояние включает поляризацию и облака потенциальных позиций и частот колебаний (т. е. энергии)».

Пожалуй, важнейшим понятием квантовой физики является понятие состояния. В широком смысле слова состояние – это множество устойчивых значений переменных параметров объекта. Под состоянием элементарной частицы обычно подразумевают её переменные параметры, причём не все, а только те, которые важны для измерения. Например, координата и импульс, если нам нужно измерить, через какую щель прошёл фотон в эксперименте Юнга. В квантовой информатике чаще всего используется такой параметр, как направление спина. Не буду сейчас объяснять, что такое спин – главное, что он может быть направлен вверх или вниз. Этого уже достаточно, чтобы сделать его физическим носителем элементарной единицы информации – бита. Проекцию спина можно измерить по трём осям (x, y или z), но мы будем всегда измерять её по одной оси (z), чтобы не усложнять. Итак, у нас есть всё, что необходимо для измерения. Чтобы убедиться в точности, мы измеряем спин одного и того же электрона много раз и получаем случайную последовательность классических битов – нулей и единиц. Но почему? Это же противоречит ньютоновскому детерминизму и принципу воспроизводимости, согласно которому при идентичных экспериментах и начальных условиях результат должен быть одним и тем же.

Увы, квантовые эксперименты воспроизводимы только статистически, а результат конкретного измерения предсказать нельзя. Например, если вероятность спина вверх равна 4/5, а вероятность спина вниз – 1/5, то в 800 случаях мы получим спин вверх, а в 200 – спин вниз. Но самое страшное даже не это. Главная проблема в том, что значение физических переменных не определено до момента измерения. Не мы не знаем, куда направлен спин, а сам спин не знает, куда он направлен. Но, в отличие от классических носителей, элементарная частица может находится в квантовой суперпозиции противоположных состояний, в которой спин будет направлен одновременно и вверх, и вниз, причём в определённой пропорции. Точнее, его направленность может принимать любое из непрерывного континуума действительных чисел между нулём и единицей включительно. Например, 0,618. Это значит, что при измерении мы с вероятностью 62% получим спин вниз (1) и с вероятностью 38% – спин вверх (0). Но мы привели упрощённый пример с одной степенью свободы, а реальное состояние частицы – это всегда целый набор параметров (наблюдаемых величин), обозначаемых не действительными числами, а операторами в гильбертовом пространстве – квадратными матрицами из комплексных чисел.

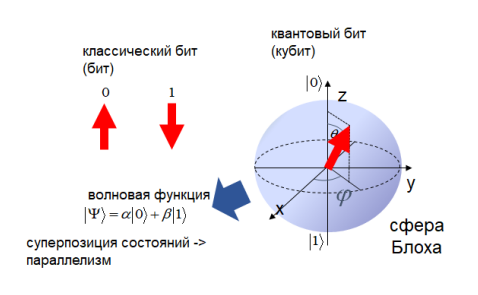
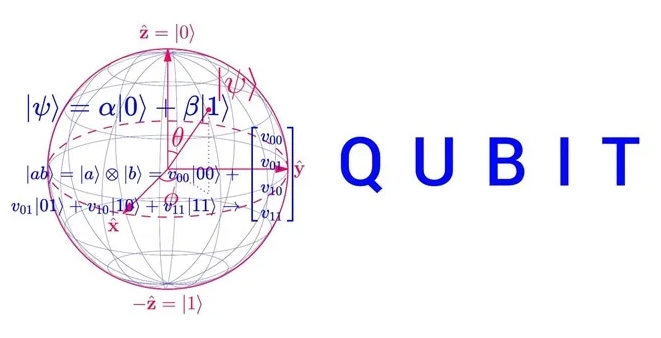
Оказывается, квантовая информация радикально отличается от классической информации – её нельзя представить в двоичном коде и измерить в битах. Единицей квантовой информации является кубит. Он является обобщением классического бита и описывается вектором состояния в двумерном гильбертовом пространстве комплексных чисел. Кубит представляет количество квантовой информации, которое может храниться в состоянии простейшей квантовой системы, например, состоянии поляризации фотона или направлении спина электрона, как в нашем примере.

В статье «Теория конструкторов» я уже кратко объяснял, чем квантовая информация отличается от классической. Во-первых, в квантовой физике действует теорема о запрете клонирования неизвестного квантового состояния. Это значит, что над кубитом нельзя осуществить логическую операцию копирования, т.е. получить копию, сохранив исходный экземпляр. В противном случае мы могли бы извлечь из одного кубита любое количество классических битов, и тем самым полностью измерить его состояние. Это позволяло бы передавать информацию на расстоянии со сколь угодно большой скоростью, что противоречит специальной теории относительности. Поэтому в реальности из одного кубита можно извлечь только один классический бит информации. Во-вторых, все остальные логические операции над кубитами должны быть обратимыми, т.е. давать на выходе значения, по которым можно воссоздать значения, которые были на входе. В статье «Информация об информации» мы определили классическую информацию как набор атрибутов физической системы, которые можно инвертировать и копировать. Теперь мы можем определить квантовую информацию как набор инвертируемых атрибутов (переменных) физической системы, по крайней мере часть из которых не может быть скопирована и все преобразования которых обратимы.

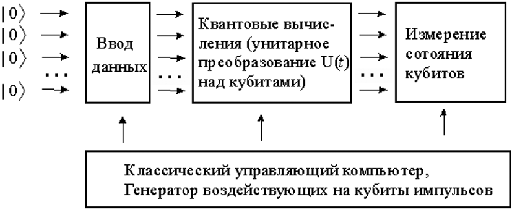
Многие ошибочно считают слово «квантовый» синонимом слова «дискретный», но в действительности квантовая механика описывает мир как непрерывную волновую функцию, а дискретные значения появляются только при измерении. Поэтому в кубите можно закодировать сколь угодно большое количество классической информации. Эту информацию можно обрабатывать и передавать, но из-за особенностей квантовых измерений можно получить доступ не более чем к одному биту. Проще говоря, на любой заданный вопрос квантовый компьютер отвечает только «да» или «нет». Чтобы этот ответ имел какой-то смысл, нужно правильно задать вопрос, то есть построить схему из логических элементов – квантовых вентилей. Подробнее я рассказывал об этих элементах в статье «Квантовый компьютер». Верхний предел количества доступной информации называется границей Холево: для n кубитов, которые могут нести большее количество классической информации благодаря квантовой суперпозиции, количество классической информации, которую можно извлечь на практике, не превышает n классических битов. Согласно теореме Холево, доступная информация в распределении вероятностей по набору альтернативных состояний кубита (матрице плотности) ограничена энтропией фон Неймана. Что это за энтропия такая, мы скоро узнаем.

Чистые квантовые состояния

Квантовые системы (элементарные частицы или кубиты, а также их совокупности) могут находиться в чистом или смешанном состоянии. Эти понятия были введены в то время, когда мир ещё делили на квантовый и классический, поэтому чистым называли состояние изолированной квантовой системы, а смешанным – когда квантовая система взаимодействует с классическим прибором или средой. Чистое состояние описывается вектором состояния (волновая функция) или полным набором квантовых чисел в данный момент времени (матрица плотности), смешанное состояние – только матрицей плотности.

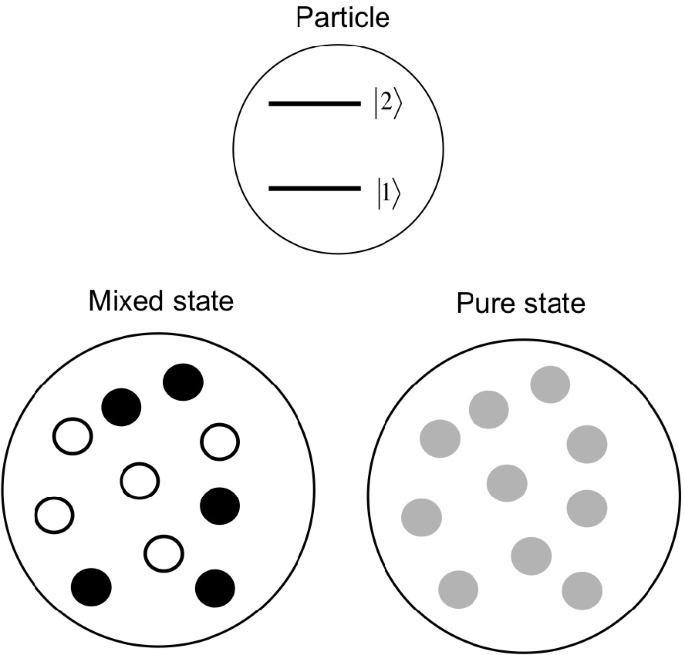
Первый постулат квантовой механики гласит, что состояние квантовой системы полностью описывается единичным вектором комплексного гильбертова пространства состояний – волновой функцией. Что это такое, вам не скажет ни один квантовый механик. Забудьте сейчас о корпускулярно-волновом дуализме, неживом-немёртвом коте Шрёдингера, облаке вероятности и о суперпозиции как расположении частицы в двух местах одновременно. У волновой функции нет классических аналогов, поэтому наш мозг просто не способен её себе представить. В случае с кубитом лучше всего визуализировать его в виде сферы Блоха, в которой северный полюс обозначает состояние 0, южный – 1, стрелка-радиус может указывать на любую точку на поверхности сферы, соответствующую чистому состоянию, а точки внутри сферы представляют смешанные состояния. Единственное, что можно сказать наверняка – волновая функция даёт максимально полное знание о квантовой системе – ничего фундаментальнее в квантовой механике нет, никаких скрытых параметров. Многочисленные эксперименты с квантовой запутанностью, о которых я рассказывал в статье «Жуткое дальнодействие», показали, что частицы на самом деле находятся в неопределённом состоянии до измерения.

Волновая функция является решением уравнения Шрёдингера, о котором речь пойдёт чуть позже. Иногда волновую функцию объясняют как волну вероятности, или соотношение вероятностей обнаружить систему в том или ином состоянии. Например, спин электрона может быть с вероятностью 62% направлен вниз, а с вероятностью 28% – вверх. Или с вероятностью 50/50 – как у честной монеты. Но это крайне упрощённое описание, потому что речь идёт не о классической вероятности, а об амплитуде вероятности, обозначаемой комплексным числом. Амплитуда вероятности может быть как положительной, так и отрицательной, и даже мнимой. Волновая функция ставит в соответствие какому-то измеряемому параметру комплексное число, угол поворота которого называется фазой. Фазы комплексных чисел отвечают за эффекты интерференции, усиления и ослабления вероятностей. В чистом состоянии вероятности могут быть когерентны и квантово интерферировать между собой. Такое чистое состояние называется когерентной (квантовой) суперпозицией.

Согласно принципу суперпозиции, результатом взаимодействия двух или более волн в одной точке пространства будет новая волна, являющаяся суммой их амплитуд. В квантовой механике суперпозиция означает возможность складывать квантовые состояния. Если у нас есть система из трёх частиц, то её следует описывать не тремя отдельными волновыми функциями от трёх переменных каждая, а одной волновой функцией от девяти переменных. Информация растёт с числом частиц не в арифметической, а в геометрической прогрессии, что является основой превосходства квантовых компьютеров над классическими. Но когерентная суперпозиция – это чистое состояние изолированной квантовой системы. Макроскопическую систему ввести в чистое состояние очень сложно: в лучшем случае это удаётся сделать только для одной степени свободы и на короткое время.

Учёные до сих пор спорят, является ли волновая функция физическим объектом или только мерой нашего знания о системе и удобным инструментом для её описания, в то время как физическая реальность имеет совершенно иное описание. Сторонники копенгагенской интерпретации вслед за Нильсом Бором считают, что волновая функция отражает лишь знание наблюдателя о квантовой системе, это просто математический инструмент, а что скрывается за ней и существует ли вообще объективная реальность, мы не знаем и никогда не узнаем. Но в обыденном представлении знание – это когда наблюдатель может охарактеризовать объект словами и количественными характеристиками. А здесь получается какое-то странное знание, когда наблюдатель не может описать систему действительными числами, измерить в классических битах, вычислить классические вероятности и объяснить сам себе, что же это значит. Субъективные вероятности обычно не выражаются комплексными числами и не взаимодействуют друг с другом – только нечто физически существующее может влиять на что-то ещё или интерферировать само с собой.

Ситуацию с квантовыми вероятностями хорошо иллюстрирует притча Станислава Лема «Путешествие третье, или Вероятностные драконы»: «…имеется три типа драконов: нулевые, мнимые и отрицательные. Все они, как было сказано, не существуют, однако каждый тип — на свой особый манер. Мнимые и нулевые драконы, называемые на профессиональном языке мнимоконами и нульконами, не существуют значительно менее интересным способом, чем отрицательные». Видимо, нулевая, отрицательная и мнимая вероятности соответствуют трём разным категориям контрфактуалов, или способам несуществования. Как бы то ни было, волновая функция вполне соответствует критерию реальности, сформулированному нами в статье «Реализм против солипсизма», и нам не остаётся ничего другого, как признать её реальным физическим объектом. Это подтверждается экспериментально. В 2011 г. группа Джеффа Лундина опубликовала в Nature статью о прямом измерении квантовой волновой функции. На самом деле измерение не совсем прямое, но всё же обратимое. Оказывается, «при слабых измерениях можно что-то узнать о волновой функции, не разрушая её полностью». Команда «использовала слабое измерение, чтобы составить карту волновой функции ансамбля идентичных фотонов, фактически не уничтожая ни один из них. Квантовая томография, напротив, отображает волновую функцию за счёт разрушения состояния». Сейчас это уже никого не удивляет: слабые измерения регулярно практикуют в работе с квантовыми компьютерами.

Физический смысл волновой функции. Правило Борна

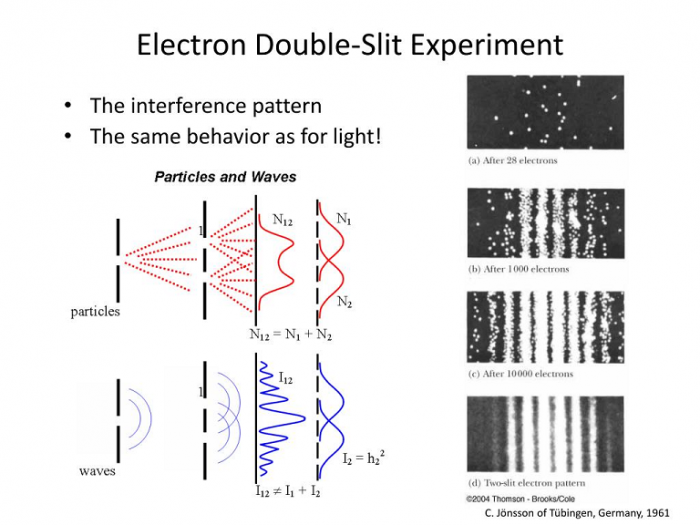
Сама по себе волновая функция ненаблюдаема и неизмерима. Мы не видим квантовую интерференцию напрямую, но видим интерференционную картину на экране в двухщелевом эксперименте. Эта картина показывает нам распределение вероятностей обнаружить электрон в той или иной точке экрана. В этом и заключается физический смысл волновой функции. В 1927 г. Макс Борн сформулировал статистическую интерпретацию волновой функции, согласно которой амплитуда волны в данной точке пространства пропорциональна вероятности обнаружения электрона в этой точке пространства. Электрон с большей вероятностью можно обнаружить там, где амплитуда больше, с меньшей вероятностью – в областях с малой амплитудой. Если амплитуда равна нулю, то в этой области электрон не будет обнаружен. Но, строго говоря, она никогда не равна нулю: квантовой физике может произойти всё, что не запрещено законами сохранения, хотя и с различными амплитудами вероятности.

Функцию плотности вероятности различных исходов измерения можно вычислить по правилу Борна, возведя модуль волновой функции в квадрат. Тем самым мы избавляемся от мнимых чисел и прочих непотребств, получая только классические положительные вероятности. Что-то должно обязательно произойти, поэтому сумма вероятностей различных исходов равна единице. Квадрат абсолютного значения амплитуды вероятности есть вероятность осуществления события, описываемого этой амплитудой. Вероятность взаимнооднозначно определяется модулем амплитуды вероятности, тогда как фаза амплитуды вероятности не имеет классического соответствия и присутствует только у волновой функции. Но если амплитуда и фаза вероятности волновой функции – это онтологическое свойство, описывающее объективную реальность, то распределение вероятностей имеет эпистемологический статус, то есть показывает, что мы знаем, а что не знаем о системе.

Правило Борна было и остаётся единственным надёжным способом рассчитать вероятность того или иного результата при измерении. Проблема в том, что оно формулируется в виде постулата и не объясняет, почему вероятность обнаружить электрон в одном месте выше, чем в другом. Только в 2019 г. Луис Масанес, Томас Галли и Маркус Мюллер смогли логически вывести правило Борна из более фундаментальных физических принципов: предположения, что ансамбли в конечномерных гильбертовых пространствах характеризуются конечным числом параметров, унитарности (обратимости) квантовых операций, инвариантности размещения частей квантовой системы при измерении (способ разделения физической системы на подсистемы является субъективным выбором наблюдателя) и уникальности каждого измерения, сводящего множество вероятностей к единственному результату.

Статистическая интерпретация Борна говорит о том, что мы в принципе не можем предсказать результат измерения. Максимум, на что можно рассчитывать – это получить статистическое распределение возможных результатов. Но, если повторять измерение много раз, его результаты всегда идеально соответствуют этому распределению и подтверждают выведенную теоретически волну вероятности. В отличие от классической механики, предсказывающей числовое значение при измерении, квантовая механика предсказывает только вероятность получить данное числовое значение при измерении. Поэтому наблюдаемая физическая величина характеризуется не численным значением, а оператором. В этом заключается второй постулат квантовой механики: каждой физической переменной соответствует определённый линейный оператор. Упрощённо, оператор – это правило, согласно которому одна волновая функция преобразуется в другую.

Смешанные и запутанные квантовые состояния

Оператором, описывающим состояние любой квантовой системы, является матрица плотности. Возьмём в качестве примера кубит, который может находиться в одном из двух собственных состояний (0 или 1) или в линейной комбинации (когерентной суперпозиции) этих состояний. Для простоты введём его в чистое состояние с равной вероятностью обнаружить спин вверх или спин вниз (50/50) – на сфере Блоха это соответствует горизонтальной стрелке. Оператором, описывающим состояние любой квантовой системы, является матрица плотности. Возьмём в качестве примера кубит, который может находиться в одном из двух собственных состояний (0 или 1) или в линейной комбинации (когерентной суперпозиции) этих состояний. Для простоты введём его в чистое состояние с равной вероятностью обнаружить спин вверх или спин вниз (50/50) – на сфере Блоха это соответствует горизонтальной стрелке. Кубит может быть описан вектором состояния: где ∣0⟩ и ∣1⟩ обозначают состояния спина вверх и спина вниз соответственно. А можно описать то же самое матрицей плотности, в которой по диагонали указаны вероятности направления спина: 0,5 для состояния вверх и 0,5 для состояния вниз. Если бы речь шла о классической системе (например, монете), недиагональные элементы были бы равны нулю, что означало бы отсутствие интерференции. Но, поскольку у нас есть интерференция, недиагональные элементы несут дополнительную информацию о системе.

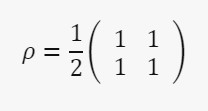
Описание квантовой системы на языке матрицы плотности необходимо в случае, когда система является частью (подсистемой) некоторой большой системы. Матрица плотности для кубита в смеси состояний ∣0⟩ и ∣1⟩ с равными вероятностями будет выглядеть так:

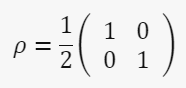
Смешанное состояние (или просто смесь) – это состояние квантовомеханической системы, в котором не задан максимально полный набор независимых физических величин, определяющих состояние системы, а определены лишь вероятности. Смесь – это когда у нас есть набор возможных состояний, и мы не знаем, в каком из них находится кубит. Смешанные состояния возникают в двух различных ситуациях при описании открытых систем, взаимодействующих с окружающей средой: когда один наблюдатель не знает, в каком состоянии приготовил систему другой наблюдатель, или когда наблюдателю нужно описать физическую систему, которая запутана с другой системой, не описывая их совместное (запутанное) состояние. Например, в смешанном состоянии находятся фотоны неполяризованного света, молекулы газа в термостате и вообще все частицы в составе неизолированных от внешней среды макроскопических объектов, включая нас с вами.

В смешанном состоянии, в отличие от чистого, различные квантовые состояния не сохраняют фазу и почти не интерферируют между собой, поэтому его называют некогерентной суперпозицией. Например, в двухщелевом эксперименте луч света находится в когерентной суперпозиции состояний «прошёл через левую щель» и «прошёл через правую щель». Эти состояния в одних местах интерферируют конструктивно, в других – деструктивно, создавая на экране интерференционную картину. Но, если фотон запутывается с детектором или внешней средой, его состояния перестают интерферировать – суперпозиция становится некогерентной, и на экране остаётся след от одной щели. Точнее, интерференция волновых функций происходит, но в таком рассинхронизированном состоянии её результат не зависит от пройденного волной расстояния. В каждой точке экрана мы получим одинаковое количество как конструктивно, так и деструктивно интерферирующих слагаемых, что в среднем даёт нулевой вклад.

Если каждая из нескольких подсистем находится в чистом состоянии, то волновая функция такой системы есть произведение волновых функций каждой из подсистем. Состояния сложной квантовой системы, которые не могут быть представлены как произведение состояний подсистем, называются запутанными. Для системы в запутанном состоянии состояния подсистем взаимозависимы, квантово коррелированы друг с другом. В этом случае мы не можем определить состояния подсистем через волновые функции или матрицы плотности так, чтобы по состояниям подсистем можно было восстановить состояние сложной системы. Когда частица или кубит квантово запутаны с другой частицей или кубитом, вместе их можно описать волновой функцией, но по отдельности – только матрицей плотности. То есть пара запутанных частиц находится в чистом состоянии, но каждая из частиц – в смешанном. При этом наблюдается корреляция между физическими величинами, относящимися к разным частицам: изменение состояния одной частицы позволяет узнать состояние другой независимо от расстояния между ними.

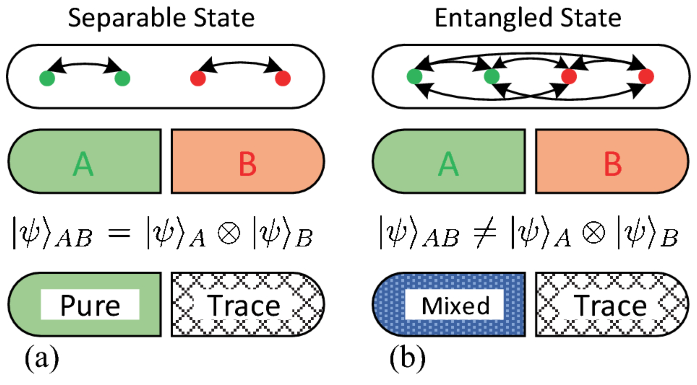Сравнение незапутанного и запутанного состояний

Частицы естественным образом запутываются при каждом взаимодействии. Например, при столкновении двух частиц у них становятся коррелированными импульсы, а при распаде одной частицы на две у них могут быть запутаны спины. Запутанные и смешанные состояния часто отождествляют, но следует помнить, что запутанным может быть только общее состояние двух кубитов, а смешанным – каждого из них по отдельности. Если у вас есть два запутанных кубита, их общее состояние может быть чистым, но состояния каждого отдельного кубита будут смешанными. Это происходит потому, что информация о состоянии каждого кубита не полностью определена – она запутана с состоянием другого кубита. Допустим, у нас есть два кубита в запутанном состоянии (состоянии Белла или состоянии ЭПР):

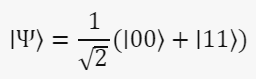
Это чистое состояние для системы из двух запутанных кубитов. Здесь ∣00⟩ и ∣11⟩ обозначают состояния, в которых оба кубита имеют спин вверх или оба кубита имеют спин вниз, соответственно. Матрица плотности для каждого кубита будет выглядеть так:

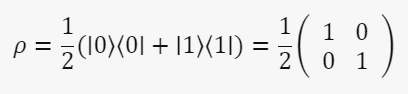
Это смешанное состояние, поскольку каждый кубит может быть найден в состоянии |0⟩ или |1⟩ с равной вероятностью, и нет определенной фазовой связи между этими двумя состояниями, о чём свидетельствуют нулевые значения недиагональных элементов матрицы. Матрица плотности для запутанного состояния двух кубитов будет выглядеть так:

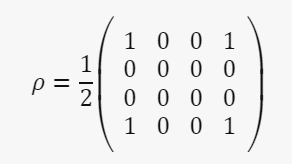
Здесь каждый элемент матрицы соответствует скалярному произведению базисных векторов. Например, элемент в первой строке и первом столбце соответствует ∣00⟩⟨00∣, а элемент в последней строке и первом столбце соответствует ∣11⟩⟨00∣.

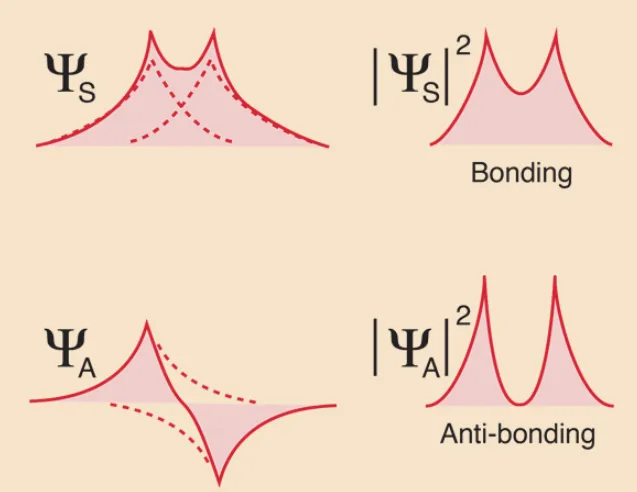Сравнение амплитуд вероятности запутанного и незапутанного состояния

Итак, матрица плотности – распределение вероятностей различных смешанных состояний системы по базису из чистых состояний. Мы не знаем, в каком чистом состоянии находится система, но знаем, с какой вероятностью какой вектор состояния ей соответствует. Смешанное квантовое состояние – статистический ансамбль чистых состояний, где система может быть в состоянии 0 с вероятностью 50% или в состоянии 1 с вероятностью 50%. Если волновая функция отображает только чисто квантовые неопределённости наблюдаемых величин, то матрица плотности включает как квантовые неопределённости (амплитуды вероятностей), так и наше незнание того, в каком именно квантовом состоянии находится система (классические вероятности). А какая величина является мерой неопределённости или нашего незнания о системе? Правильно – энтропия.

Энтропия фон Неймана

Энтропия фон Неймана является обобщением классической энтропии Больцмана-Гиббса на квантовомеханические системы. То есть термодинамическая энтропия – её предельный случай для систем с большим количеством частиц, тогда как сама энтропия фон Неймана применима даже к одной частице. Здесь любой читатель вправе спросить: ну о какой энтропии одной частицы может идти речь, если энтропия, как и температура – свойство большого количества частиц? В классической физике – да, термодинамической энтропией обладают только макроскопические системы с большим числом частиц, а энтропия отдельной частицы равна нулю. Но есть же ещё информационная энтропия Шеннона как мера неопределённости сообщения. В классической теории информации, которую мы разбирали в предыдущих двух статьях, энтропия Шеннона измеряет количество неопределённости в значении случайной величины в битах. Например, в случае двоичной случайной величины с двумя равновероятными возможностями энтропия Шеннона равна 1 бит, что отображает максимальную неопределённость. Энтропия Шеннона применима только к информации в классических системах, а энтропия фон Неймана – это её обобщение на квантовые системы. То есть речь идёт о неопределённости состояния частицы или кубита.

С точки зрения наблюдателя, любая система обладает энтропией, отображающей, как много информации о ней не может быть получено при взаимодействии с ней. Энтропия Больцмана показывает, сколько информации вам не известно о макроскопической системе. Энтропия Шеннона показывает, сколько информации вам не известно о сообщении. А энтропия фон Неймана показывает, сколько информации вам не известно о квантовой системе. Но, как я уже говорил в предыдущих видео, энтропия – объективная величина, её лучше рассматривать не с точки зрения наблюдателя (как меру неизвестной ему информации о системе), а с точки зрения самой системы – как много микросостояний системы дают одни и те же макроскопические свойства. Если система находится в чистом состоянии, а подсистемы – в смешанном, их состояние неопределены, как если бы у них были волновые функции, неизвестные наблюдателю. Эта неопределённость и есть энтропия фон Неймана.

Джон фон Нейман (1903–1957)

Энтропия фон Неймана измеряет, насколько состояние системы является смешанным. Она применима к любому квантовому состоянию и может быть вычислена для любой матрицы плотности. Частным случаем энтропии фон Неймана применительно к запутанным состояниям является энтропия запутанности. Для чистых состояний (например, |Ψ⟩=|↑⟩A|↓⟩B) она равна нулю, что означает отсутствие запутанности: измерение кубита B ничего не сообщает о кубите A. Если она близка к максимальному значению (1), это свидетельствует о сильной запутанности: измерение кубита B позволяет узнать много нового о состоянии кубита A. Иначе говоря, энтропия запутанности – мера того, насколько измерение кубита B уменьшает ваше незнание состояния кубита A. Это основной способ количественной оценки запутанности между двумя объектами. Согласно формуле, энтропия фон Неймана – это след (сумма диагональных элементов матрицы) от произведения матрицы плотности на её логарифм:

Я привожу эту формулу только для того, чтобы вы сравнили её с формулами энтропии Шеннона и Больцмана. Похоже, правда?

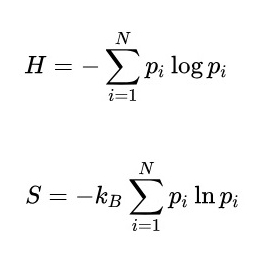
Очевидно, все три вида энтропии как-то связаны. Есть даже гипотеза, что электромагнитные, слабые, сильные и гравитационные взаимодействия – всего лишь следствие и первое приближение энтропийных взаимодействий, но речь сейчас не об этом.

Квантовая энтропия, в отличие от классической, обладает таким свойством, как субаддитивность. Это значит, что энтропия системы может быть меньше суммарной энтропии её элементов. И не просто меньше – система может находится в чистом состоянии и обладать нулевой энтропией, а её составляющие при этом будут в смешанных состояниях с ненулевой энтропией. Это когда вы знаете всё, что можно знать о системе, но ничего не знаете о её составляющих. В классической системе такого быть не может: если система находится в определённом состоянии с нулевой энтропией, то все её части также обладают нулевой энтропией. Если мы знаем состояние целого, то мы знаем и состояние его частей. Из-за субаддитивности при любом разделении квантовой системы на части энтропия будет сохранятся или увеличиваться. Чистое состояние сложной системы в общем случае не восстановимо по состояниям подсистем. Чистое состояние системы может дать смешанное для подсистемы, а смешанное состояние системы даёт чистое для подсистемы.

В классическом случае мы имеем один бит энтропии Шеннона, когда мы не знаем, в каком из двух состояний находится бит информации: 0 или 1. В квантовом случае кубит может находится в квантовой суперпозиции состояний |0> + |1>, и его энтропия при этом будет равна нулю. Когда два кубита запутываются, их состояния становятся скоррелированными, и каждый из них по отдельности оказывается в максимально неопределённом (смешанном) состоянии (или |0>, или |1>), что соответствует одному биту энтропии фон Неймана. Но система из двух кубитов остаётся в чистом состоянии |00> + |11>, с нулевой энтропией. И хотя два запутанных кубита делят между собой только один бит энтропии, при измерении они могут давать противоположные ответы «да/нет» на бесконечное количество двоичных вопросов, соответствующих бесконечному набору осей, относительно которых их можно измерить.

Согласно теореме Эберхарда, в квантовой системе, которая описывается матрицей плотности, никакое измерение наблюдаемых, связанных только с подсистемой A, не влияет на результат измерения любых наблюдаемых, которые связаны только с подсистемой B. Запутанность – величина ненаблюдаемая, о её наличии можно узнать, только измерив по очереди два кубита и получив противоположные спины. Как мы уже рассказывали в ролике «Жуткое дальнодействие», никакой нелокальности здесь нет, измерение первого спина может увеличить наши знания о втором, но не изменит его состояния, пока его не измерит другой наблюдатель. Это значит, что невозможно мгновенно передать информацию от первого спина ко второму. Можно измерить один из запутанных кубитов так, чтобы второй с равной вероятностью оказался равным вверх или вниз. Второй кубит не имеет собственной волновой функции: он уже находится в определённом состоянии, каждый в своей ветви общей волновой функции. Но второй наблюдатель ещё не знает, в какой из этих ветвей окажется, для него они равновероятны. Следовательно, второй кубит обладает ненулевой энтропией даже до того, как был измерен первый кубит.

Принцип унитарности операторов

В разных формулировках третий постулат квантовой механики звучит так: «эволюция замкнутой квантовой системы описывается унитарным оператором» или «волновая функция эволюционирует согласно уравнению Шрёдингера». Естественно, речь идёт не о дарвиновской эволюции, а о физической эволюции как изменении системы со временем. Фактически третий постулат – это и есть закон сохранения информации в квантовой механике. Он сводится к тому, что в квантовой механике все операции унитарны, то есть одно состояние суперпозиции линейно переходит в другое, и этот процесс обратим во времени. Переход из одного состояния к другому описывается оператором. Состояние квантовой системы (квантовая суперпозиция) математически описывается как вектор в гильбертовом пространстве (пространстве состояний), а эволюция системы – как оператор, осуществляющий унитарное преобразование этого вектора.

Унитарное преобразование – это обобщение поворота, а унитарный оператор – обобщение матрицы поворота. Унитарность эволюции замкнутой квантовой системы включает три фундаментальных принципа квантовой теории: линейности, сохранения вероятности (изометричности) и обратимости времени. Линейность преобразования требует, чтобы преобразование переводило состояние кубита, представленное суммой двух состояний кубита, в новое состояние кубита, которое является суммой преобразованных состояний кубита. Это ни что иное, как принцип суперпозиции. Сохранение вероятности означает, что события не исчезают и не появляются новые. Со временем могут меняться лишь распределения вероятностей между теми или иными альтернативами, но сумма вероятностей альтернативных событий всегда равна 1 (100%). Обратимость означает, что волновая функция может одинаково разворачиваться как вперёд, так и назад во времени. Два разных квантовых состояния (координата, импульс) всегда переходят в два других состояния, но никогда не переходят в одно, иначе было бы невозможно их воссоздать, то есть прокрутить процесс назад во времени. По данному значению волновой функции можно определить её значение в любой предыдущий и любой последующий момент времени.

Эволюция замкнутой системы является разновидностью симметрии – сдвига по времени, порождаемого оператором энергии – гамильтонианом. Временную эволюцию волновой функции описывает уравнение Шрёдингера, инвариантное обращению времени. Уравнение Шрёдингера – квантовый аналог классических законов Ньютона. В переводе на естественный язык оно звучит так: «Скорость изменения волновой функции пропорциональна энергии квантовой системы», или, в более строгой формулировке, «волновая функция может описывать состояния с различными энергиями, и, согласно уравнению Шрёдингера, высокоэнергетические части волновой функции эволюционируют стремительно, а низкоэнергетические – очень медленно». Уравнение Шрёдингера применимо только к замкнутой системе в чистом состоянии. Если же частица взаимодействует с другими частицами, то есть находится в смешанном состоянии, волновая функция относится уже ко всей системе взаимодействующих частиц и зависит от всех их динамических переменных.

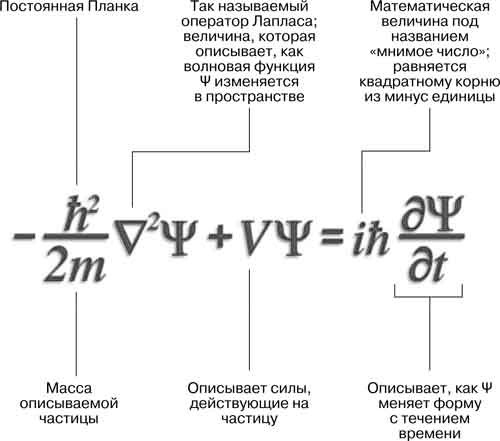
Неунитарные операторы эволюции для изолированной квантовой системы в квантовой механике запрещены. Для незамкнутой системы, например, в случае квантового измерения, из трёх составляющих унитарности остаётся в силе только сохранение вероятности, однако коллапс волновой функции нелинейный и необратим во времени. Получается, что при измерении принцип унитарности как бы соблюдается, но не совсем. Как же так? Здесь мы подошли к четвёртому, самому спорному постулату квантовой механики: «при измерении физической величины получается одно из собственных значений оператора, представляющего эту величину» или «вектор состояния переходит в один из базисных векторов, соответствующий измеренному собственному значению». Постулат об измерении вступает в конфликт с постулатом об унитарной эволюции квантовых систем во времени, поскольку в результате измерения уничтожается информация об исходных вероятностях: два комплексных числа переходят в 1 и 0. После измерения мы не можем воссоздать компоненты вектора состояния (амплитуды вероятностей), если нам заранее не было известно состояние системы.

О проблеме измерения и способах её решения я уже рассказывал в статье «Интерпретации квантовой механики» на примере кота Шрёдингера, но тема интересная и требует более глубокого погружения. Поэтому в следующей статье мы выясним, сохраняется ли информация при измерении, может ли коллапс волновой функции быть причиной необратимости времени, является ли квантовая механика самосогласованной теорией и какая интерпретация даёт лучшее решение проблемы измерения. Также мы проясним смысл чистых и смешанных состояний, энтропии фон Неймана, принципа унитарности и других понятий этой статьи на примере эксперимента «друг Вигнера» и его вариаций.

Вывод

Таким образом, все известные на сегодняшний день физические явления сохраняют информацию – это следует из фундаментальных принципов симметрии физических преобразований. Конечно, теорема Нётер, CPT-инвариантность, уравнение Шрёдингера и вообще весь математический аппарат квантовой механики применимы только в плоском пространстве-времени Минковского, где отсутствует гравитация. В искривлённом пространстве-времени Лоренца всё это работает немного иначе, даже закон сохранения энергии может не соблюдаться. Но принцип сохранения информации должен оставаться в силе даже в экстремальных условиях Большого взрыва или вблизи горизонта событий чёрной дыры. Некоторые учёные считали исключением из этого правила предсказанное в 70-е гг. излучение Хокинга, пока сам Хокинг не признал в 2004 г. своё поражение в знаменитой «битве при чёрной дыре». Подробнее мы напишем об этой истории в статье о термодинамике чёрных дыр.