В 2013 году группа молекулярных биологов из США исследовали очень интересную форму эндоплазматической сети — органоида внутри эукариотической клетки. Мембрана этого органоида состоит из плоских листов, соединённых спиральными «пандусами», словно рассчитанными в программе 3D-моделирования. Это так называемые рампы Терасаки. Спустя три года работу биологов заметили астрофизики. Они были поражены: ведь точно такие структуры присутствуют внутри нейтронных звёзд. Так называемая «ядерная паста» состоит из параллельных листов, соединённых спиральными формами.

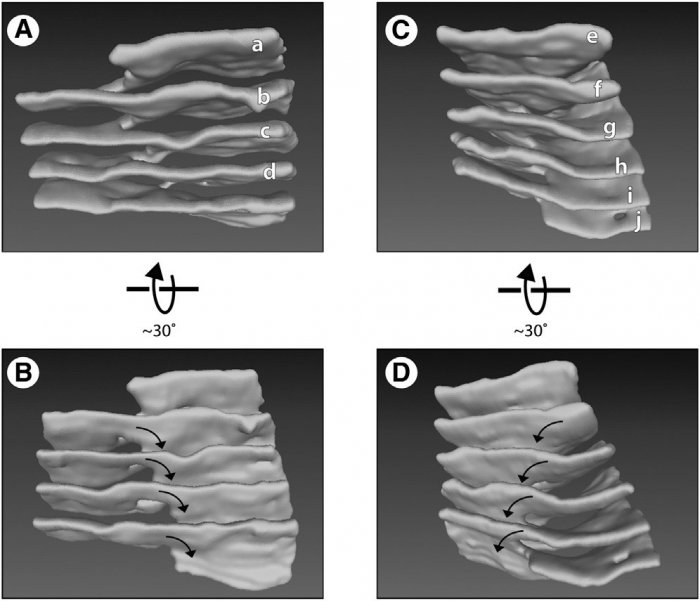
Удивительное структурное сходство живых клеток и нейтронных звёзд — откуда оно взялось? Очевидно же, что между живыми клетками и нейтронными звёздами нет прямой связи. Просто совпадение?

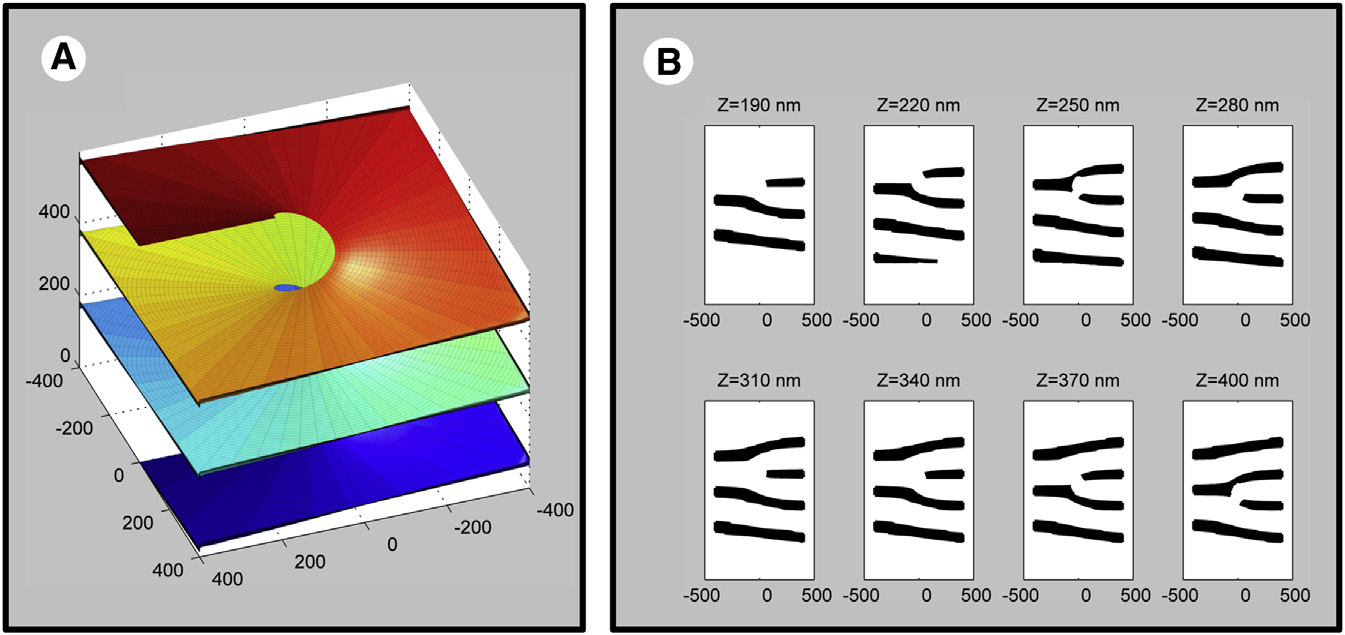Модель спиральных соединений между плоскими листами мембраны в эукариотической клетке

Есть предположение, что законы природы действуют на все объекты микро- и макромира таким образом, что некоторые наиболее оптимальные формы и конфигурации проявляются как будто сами собой. Другими словами, объекты физического мира подчиняются скрытым математическим законам, лежащем в основе всего мироздания.

Посмотрим ещё на несколько примеров, которые подтверждают эту теорию. Это примеры, когда разные по сути материальные объекты проявляют схожие свойства.

Например, впервые наблюдаемые в 2011 году акустические чёрные дыры проявляют такие же свойства, какими в теории должны обладать настоящие чёрные дыры. В первой экспериментальной акустической чёрной дыре бозе-эйнштейновский конденсат из 100 тыс. атомов рубидия раскрутили до сверхзвуковой скорости таким образом, что отдельные части конденсата преодолели звуковой барьер, а соседние — нет. Граница этих частей конденсата моделировала горизонт событий чёрной дыры, где скорость потока в точности равна скорости звука. При температурах около абсолютного нуля звук начинает вести себя как квантовые частицы — фононы (вымышленная квазичастица олицетворяет собой квант колебательного движения атомов кристалла). Оказалось, что «звуковая» чёрная дыра поглощает частицы точно так же, как настоящая чёрная дыра поглощает фотоны. Таким образом, поток жидкости действует на звук так же, как настоящая чёрная дыра действует на свет. В принципе, звуковую чёрную дыру с фононами можно рассматривать как своеобразную модель настоящего искривления в пространстве-времени.

Если посмотреть шире на структурные сходства в различных физических явлениях, то можно увидеть в природном хаосе удивительный порядок. Все разнообразные природные феномены, по сути, описываются простыми базовыми правилами. Математическими правилами.

Взять фракталы. Это самоподобные геометрические формы, которые можно поделить на части так, что каждая часть хотя бы приблизительно является уменьшенной копией целого. Один из примеров — знаменитый папоротник Барнсли.

Папоротник Барнсли строится при помощи четырёх аффинных преобразований вида:

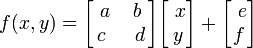
Данный конкретный лист сгенерирован со следующими коэффициентами:

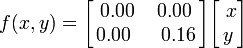
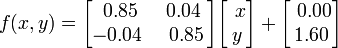
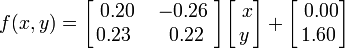
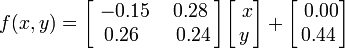
В окружающей нас природе такие математические формулы встречаются повсеместно — в тучах, деревьях, горных грядах, кристалликах льда, мерцающем пламени, в морском побережье. Это примеры фракталов, структура которых описывается относительно простыми математическими вычислениями.

Галилео Галилей ещё в 1623 году говорил: «Вся наука записана в этой великой книге — я имею в виду Вселенную, — которая всегда открыта для нас, но которую нельзя понять, не научившись понимать язык, на котором она написана. А написана она на языке математики, и её буквами являются треугольники, окружности и другие геометрические фигуры, без которых человеку невозможно разобрать ни одного её слова; без них он подобен блуждающему во тьме».

На самом деле математические правила проявляют себя не только в геометрии и визуальных очертаниях природных объектов, но и в других законах. Например, в нелинейной динамике численности популяции, скорость прироста которой динамически снижается при приближению к естественному пределу экологической ниши. Или в квантовой физике.

Что касается самых известных математических констант — например, числа пи, — то вполне естественно, что оно широко встречается в природе, потому что соответствующие геометрические формы являются наиболее рациональными и подходящими для многих природных объектов. В частности, фундаментальной физической константой стало число 2π. Оно показывает, чему равен угол поворота в радианах, содержащийся в одном полном обороте при вращении тела. Соответствено, данная константа повсеместно встречается в описании вращательной формы движения и угла поворота, а также при математической интерпретации колебаний и волн.

Например, период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен

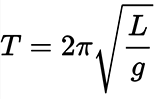
В условиях вращения Земли плоскость колебаний маятника будет медленно поворачиваться в сторону, противоположную направлению вращения Земли. Скорость вращения плоскости колебаний маятника зависит от его географической широты.

Число пи является составной частью постоянной Дирака — редуцированной постоянной Планка, основной константы квантовой физики, которая связывает две системы единиц — квантовую и традиционную. Она связывает величину кванта энергии любой линейной колебательной физической системы с её частотой.

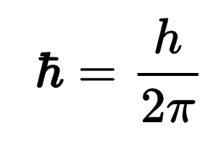
Соответственно, число пи входит в фундаментальный постулат квантовой механики — принцип неопределённости Гейзенберга.

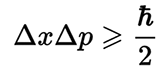
Число пи используется в формуле постоянной тонкой структуры — ещё одной фундаментальной физической постоянной, характеризующей силу электромагнитного взаимодействия, а также в формулах гидромеханики и т.д.

В природном мире можно встретить и другие математические константы. Например, число e, основание натурального логарифма. Эта константа входит в формулу нормального распределения вероятностей, которое задаётся функцией плотности вероятности:

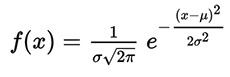
Нормальному распределению подчиняется множество природных явлений, в том числе многие характеристики живых организмов в популяции. Например, распределение размеров организмов в популяции: длина, рост, площадь поверхности, вес, артериальное давление у людей и многое другое.

Пристальное наблюдение за окружающим миром показывает, что математика — вовсе не сухая абстрактная наука, как может показаться на первый взгляд. Совсем наоборот. Математика — это основа всего живого и неживого мира вокруг. Как верно заметил Галилео Галилей, математика — это язык, на котором с нами говорит природа.