Американские физики упорядочили систему из 50 атомов цезия, помещенных в трехмерную оптическую ловушку, с помощью реального аналога демона Максвелла. В результате энтропия системы уменьшилась почти в 2,5 раза. Ранее ученым удавалось упорядочивать атомы только в одномерных и двумерных решетках. Статья опубликована в Nature, кратко о ней рассказывает раздел журнала News & Views.

В 1867 году британский физик Джеймс Максвелл предложил простой мысленный эксперимент, который, казалось бы, нарушает второй закон термодинамики. В этом эксперименте рассматривается сосуд, заполненный газом и разделенный перегородкой с маленькой дверкой, сквозь которую может пройти только одна молекула газа за раз. Около дверки сидит «вахтер», который может управлять ее состоянием, — демон Максвелла. Если к дверке справа подлетает «холодная» молекула с низкой скоростью, демон пропускает ее. Если подлетает «горячая» молекула, скорость которой выше среднеквадратичной скорости молекул в левой половине сосуда, демон оставляет дверку закрытой. В противоположную сторону дверка работает наоборот. В результате скорость молекул в левой половине сосуда постепенно уменьшается, а в правой — увеличивается. Другими словами, беспорядок в системе уменьшается, а энтропия увеличивается, хотя работа над газом не производится.

Казалось бы, это противоречит второму закону термодинамики, который утверждает, что энтропия замкнутой системы не может убывать. Тем не менее, в конце XX века было замечено, что для работы демона Максвелла необходимо собирать информацию о скорости частиц системы, что приводит к неизбежному увеличению энтропии. Если аккуратно рассмотреть систему, включая в нее демона, окажется, что рост энтропии из-за сбора информации перевешивает уменьшение за счет разделения молекул, то есть суммарная энтропия системы все-таки увеличивается. Таким образом, работа демона Максвелла не нарушает второй закон термодинамики.

Долгое время эксперимент Максвелла считался чисто умозрительным — казалось бы, невозможно построить демона, который умеет сортировать частицы по скоростям. Однако в 2009 году ученым впервые удалось реализовать этот эксперимент на практике, используя в качестве демона систему из двух лазеров. Один из лазеров отталкивает частицы, которые находятся в некотором определенном состоянии, а другой лазер переводит их в это состояние; в результате частицы собираются в одной половине сосуда, и система становится более упорядоченной. Тем не менее, энтропия системы в этих экспериментах уменьшалась незначительно, либо в «охлаждении» участвовало не более четырех частиц. Кроме того, ученым удавалось упорядочить частицы только в одном или двух измерениях.

На этот раз группа исследователей под руководством Дэвида Вайса (David Weiss) добилась гораздо большего успеха — им удалось упорядочить около 50 атомов, помещенных в трехмерную оптическую ловушку, уменьшив при этом энтропию системы почти в 2,5 раза. В оптической ловушке атомы захватываются с помощью двух поляризованных лазеров, которые создают периодический удерживающий потенциал. В этом эксперименте ученые использовали лазеры с длиной волны 839 нанометров, которые создавали решетку с шагом около 4,9 микрометров, и помещали в нее атомы цезия, переведенные в состояние с квантовыми числами l = 4 (орбитальное квантовое число) и m = −4 (магнитное квантовое число). Изначально атомы были случайно распределены по решетке размером 5×5×5, однако в конце эксперимента сжимались в подрешетку размером 5×5×2 или 4×4×3.

Схема переноса частиц в подрешетку. A. Kumar et al. / Nature

Чтобы перемещать атом по решетке, ученые придерживались следующей последовательности действий. На первом шаге они переводили атом, который требовалось передвинуть, в состояние с квантовыми числами l = 3, m = −3. Затем исследователи поворачивали поляризацию одного из пучков с помощью пластинки λ/4, в результате чего атомы, находящиеся в разных состояниях, смещались в противоположные стороны. После этого ученые переводили передвинутый атом обратно в состояние с l = 4, m = −4 и возвращали исходную поляризацию лазеров. Чтобы «сжать» исходную конфигурацию атомов в подрешетку меньшего размера, физики стабилизировали систему в плоскости xy, находили пустые места в одной из конечных плоскостей и заполняли их атомами из других слоев.

Результат упорядочивания атомов в подрешетку размером 4×4×3. A. Kumar et al. / Nature

Результат упорядочивания атомов в подрешетку размером 5×5×2. A. Kumar et al. / Nature

В результате ученым удавалось получить практически полностью заполненные подрешетки: средний коэффициент их заполнения составлял 0,97 и 0,95, а вероятность получить подрешетку без пустых мест — 32 процента и 27 процентов для подрешеток 5×5×2 и 4×4×3 соответственно. Энтропия системы при такой сортировке уменьшалась примерно в 2,44 раза, а средняя энтропия на частицу в конечной системе была примерно равна 0,75kB. Кроме того, ученые численно рассчитали с помощью метода Монте-Карло число шагов, которые нужно выполнить для упорядочивания больших систем; оказалось, что оно растет как кубический корень из числа частиц системы.

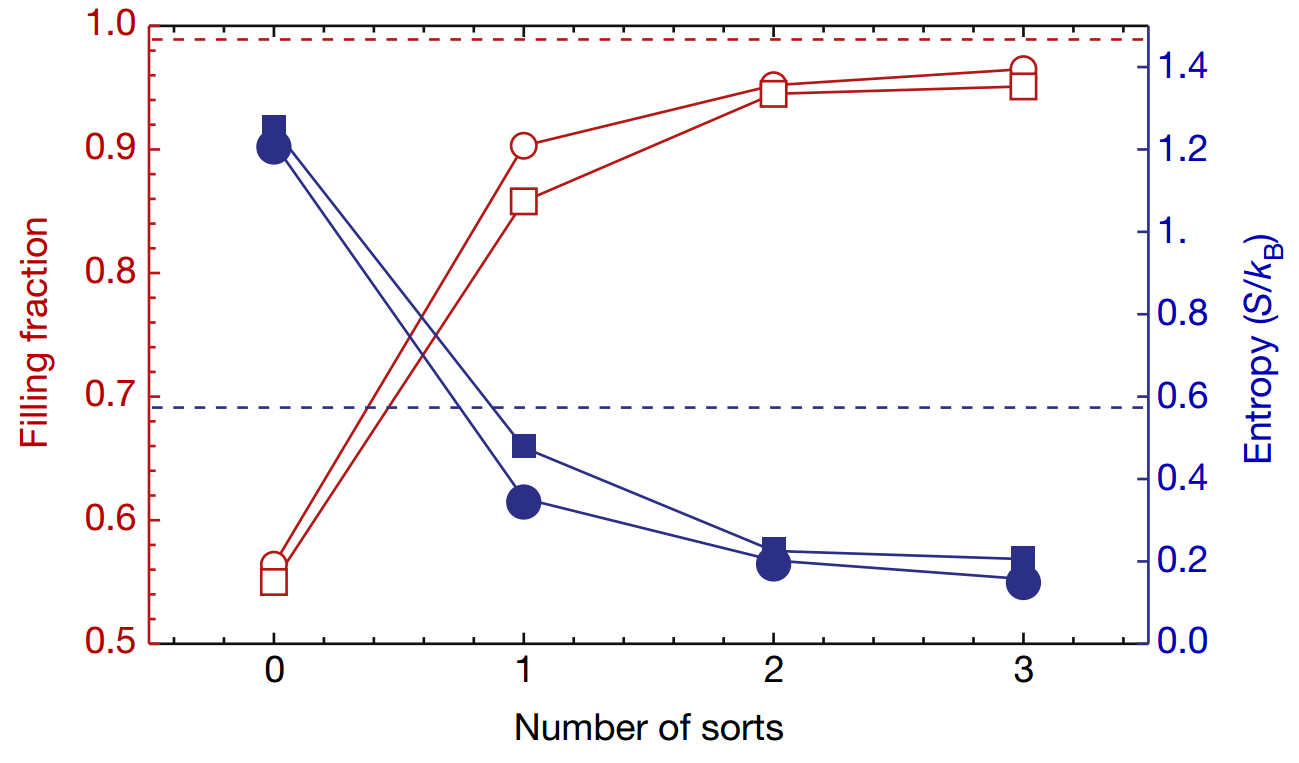Зависимость коэффициента заполнения (красный) и энтропии системы (синий) от числа шагов упорядочивания. A. Kumar et al. / Nature

Авторы статьи считают, что их разработка поможет построить универсальный квантовый компьютер. В частности, ученые предлагают реализовать торический код Китаева на двумерных подрешетках в двумерных или трехмерных решеточных калибровочных теориях.

«Усовершенствованный» вариант демона Максвелла — это двигатель Силарда, который перерабатывает информацию о системе в работу, сохраняя ее температуру постоянной. В марте 2018 года мы писали о том, как такой двигатель работает для систем взаимодействующих бозонов. Кроме того, аналог демона Максвелла также существует для сыпучих жидкостей и газов, частицы которых могут «цепляться» друг за друга и склеиваться. Если насыпать такую жидкость в коробку, разделенную перегородкой с отверстием, и потрясти систему, то частицы постепенно соберутся в одной части коробки. Более того, недавно математики показали, что сыпучие жидкости могут разогреваться вопреки уменьшению энтропии, уменьшая число степеней свободы за счет слипания частиц.

Подробно прочитать про предыдущие реализации демона Максвелла на практике можно в статье Алексея Левина «Демон Максвелла: наука невозможного», а про другие мысленные эксперименты — в материале «Не вставая с дивана».

Автор: Дмитрий Трунин