Размышления на тему искусственного интеллекта посещают умы великих людей уже многие столетия. С течением времени и развитием технологий размышления превратились в реализацию, теории в практику, а научная фантастика во вполне реальное будущее человечества. Основная суть ИИ это помощь человеку. Другими словами умные машины должны служить человеку в полной мене, не нарушая основных законов робототехники, которые высказал небезызвестный Айзек Азимов. Но подобное взаимодействие, если рассуждать приземленно, имеет лишь один вектор: человек сказал — ИИ выполнил. То есть работа искусственного интеллекта нацелена на благо лишь человека. А что если ИИ будет думать в русле блага для обеих сторон взаимодействия? Как научить машину искать компромисс, договариваться и даже торговаться с человеком? Что ж, именно на эти вопросы и дает ответы сегодняшнее исследование, в котором был создан алгоритм, позволяющий машине достигать взаимовыгодного соглашения с человеком. Давайте же подробнее рассмотрим эти вопросы. Поехали.

Идея исследования

Исследователи отмечают, что с тех самых пор, когда Тьюринг заговорил об искусственном интеллекте, человек пытается создать машину, способную в чем-то его превзойти. Все мы так или иначе знакомы с многочисленными конкурсами, соревнованиями и экспериментами, когда человек соревнуется с машиной (шахматы, покер и даже боевые искусства). Однако доселе крайне малое внимание уделялось иному виду взаимодействия человека и машины. Ведь не всегда в жизни есть только победа или поражение. Порой нужен тот самый консенсус, когда удовлетворяются потребности и/или желания двух сторон. Рассматривать работу ИИ исключительно с позиции «да или нет» — неверно, ведь всегда есть вариант «наверное».

Ученым удалось создать алгоритм, который способен оценить ситуацию, взвесить все за и против, распределить приоритеты и достичь компромисса. Для проверки работы алгоритма использовались повторяющиеся *стохастические игры**.

Стохастическая игра * — повторяющаяся игра с одним или более игроками, когда ее состояние постоянно меняется в случайном порядке.

Создание алгоритма, способного работать в столь «плавающих» условиях, задача не из легких. Дабы работать эффективно, алгоритм должен обладать некоторыми особенностями. Далее о них подробнее. Во-первых, алгоритм не должен быть предметно-ориентированным, то есть он должен работать в неограниченном числе вариантов сценариев (в данном случае, игры). Эта особенность названа учеными «всеобщность».

Во-вторых, алгоритм должен научиться выстраивать успешные связи с любыми людьми / алгоритмами без предварительного ознакомления с их поведением. Это «гибкость». Чтобы достичь такого, алгоритм должен учитывать, что практически всегда его партнер-оппонент придерживается эксплуатационного поведения, то есть хочет использовать алгоритм исключительно себе во благо. Как следствие, он должен определять, когда и как привлечь к сотрудничеству того, кто вероятнее всего не намерен сотрудничать.

И наконец, в-третьих, алгоритм должен действовать быстро, особенно играя с человеком. Эта особенность именуется «скорость обучения». На словах все очень красиво, понятно и просто. А на деле достижение подобных характеристик сопряжено со сложностями. Не говоря уже о том, что умение подстраиваться под оппонента может быть усложнено тем, что сам оппонент умеет подстраиваться. Это есть проблема, поскольку два адаптивных алгоритма, несмотря на все свои попытки подстроиться друг под друга, не могут достичь компромисса.

Также ученые отмечают, что во время взаимодействия между двумя людьми одними из важных инструментов достижения взаимовыгодных результатов являются вещи, которые сложно связать с машиной, это интуиция, эмоции, инстинкты и прочее. Было доказано, что «cheap talk» («дешевые разговоры») сильно сопутствуют взаимовыгодному результату.

Дешевые разговоры (cheap talk) * — в теории игр это взаимодействие между игроками, которое напрямую не влияет на исход игры. Другими словами «разговор не по теме».

Исследователи решили внедрить это в свой алгоритм, что помогает ему лучше справляться с вычислениями сложных ситуаций и вырабатывать общее с человеком представление о ситуации. Хотя доселе остается не совсем понятно, как алгоритм будет реализовывать подобные «навыки» в сопряжении со своими основными особенностями (гибкость, всеобщность, скорость обучения). Основной задачей исследования является изучить как можно больше существующих алгоритмов, разработать алгоритм на базе машинного обучения с механизмом реагирования на сигналы и их генерации на уровне понятном человеку, а также провести множество экспериментальных игровых партий для демонстрации обучаемости алгоритма и его способности подстраиваться под разных оппонентов (людей или других алгоритмов).

Проведение и результаты исследования

Алгоритмы стратегического поведения в повторяющихся играх присутствуют во многих аспектах жизни общества: экономика, эволюционная биология, ИИ и т.д. На данный момент создано много таких алгоритмов, каждый из которых обладает своим набором достоинств. Естественно, ученые решили использовать их для разработки своего алгоритма. Таким образом было выбрано 25 алгоритмов. Было выделено 6 показателей эффективности на базе трех вариантов игры: 100, 1000 и 50000 раундов. Показатели эффективности:

• среднее значение Round-Robin *;
• лучший результат по очкам;
• худший результат по очкам;
• динамика репликатора *;
• турнир группа-1;
• турнир группа-2.

Round-Robin * — тип игрового взаимодействия, когда во время раунда каждый из участников поочередно играет со всеми другими участниками.

Уравнение-репликатор * — детерминированная монотонная нелинейная игровая динамика, используемая в эволюционной теории игр.

Первый показатель (среднее значение Round-Robin) позволяет понять насколько хорошо алгоритм способен устанавливать выгодные взаимосвязи с разнообразными игровыми партнерами.

Второй показатель (лучший результат по очкам) это число алгоритмов-партнеров, в игре с которыми исследуемый алгоритм заработал наибольшее число очков. Выражается в процентах. Этот показатель отображает как часто алгоритм будет желанным выбором, учитывая информацию об алгоритме партнера по игре.

Третий показатель (худший результат по очкам) это оценка способности алгоритма связывать свои потери (промахи, ошибки).

Оставшиеся три показателя нацелены на определение устойчивости алгоритма для разных групп населения.

К примеру, турнир (группа-1) это череда партий, в которых алгоритмы разделены на 4 группы. Лидеры из каждой группы переходят в финал, где определяется единственный победитель. А вот в турнире группы-2 из каждой группы выбираться два лучших алгоритма, которые переходят в полуфинал, а дальше победители переходят в финал, где и определяется единственный лучший алгоритм.

По словам ученых ни один из выбранных алгоритмов (25 штук) ранее не участвовал в столь масштабной проверке (множество партнеров и измеряемых показателей). Такая проверка показывает насколько хорошо каждый из алгоритмов работает в условиях нормальной игры с 2 участниками, а не «программируется» под определенный сценарий.

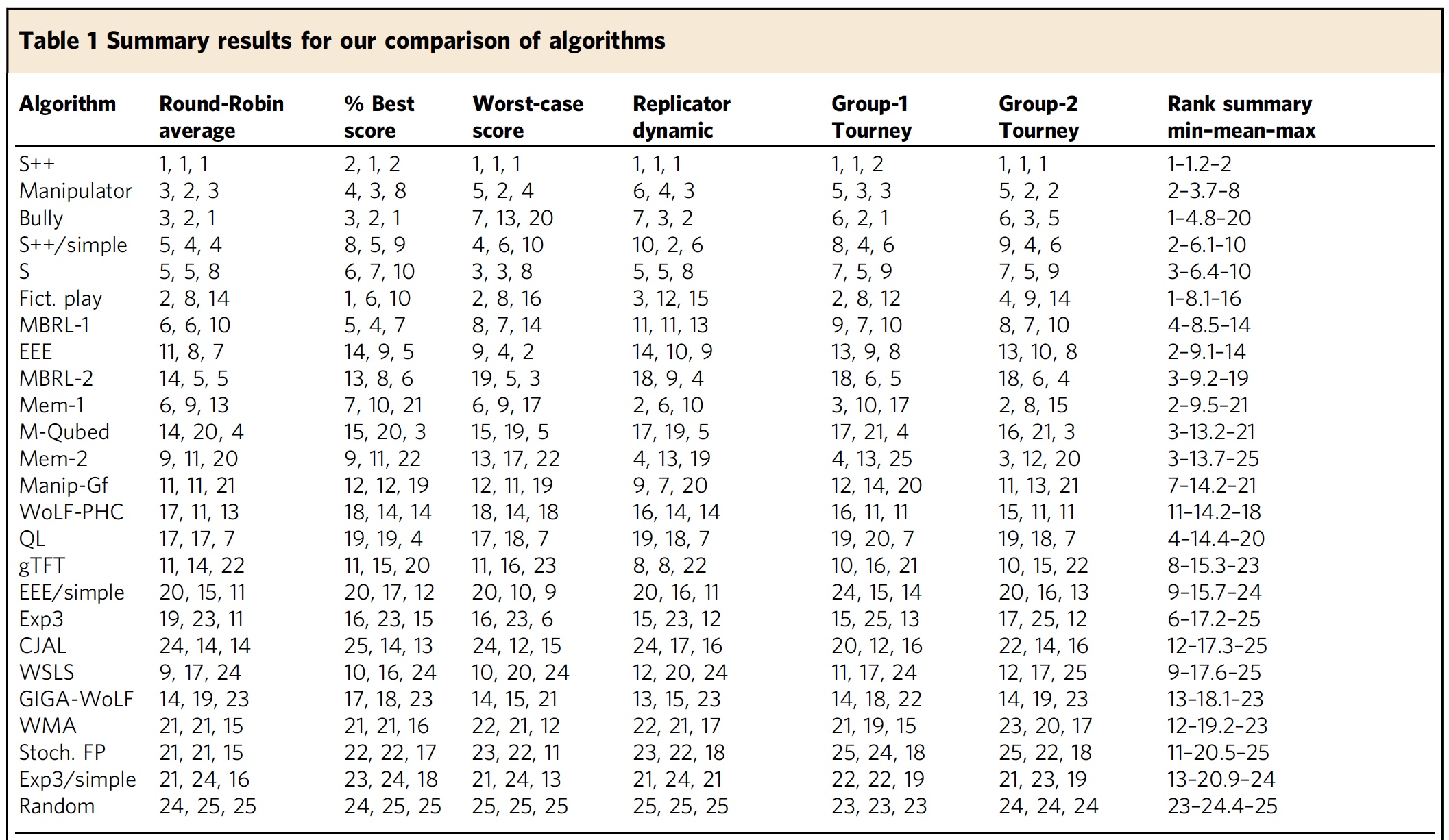Таблица №1: результаты экспериментов с участием 25 разных алгоритмов стратегического поведения.

Полученные результаты это лишь инструмент, позволяющий глубже понять плюсы и минусы того или иного алгоритма. К примеру, алгоритмы gTFT, WSLS, Mem- 1 и Mem-2 показали отличные результаты в «дилемме заключенного» *.

Дилемма заключенного * — в теории игр состояние, когда игроки не всегда готовы сотрудничать, даже если это будет им выгодно. В таком случае у игрока («заключенного») в приоритете свои интересы, и он не думает о выгоде других.

Однако эти же алгоритмы показали плохие результаты во всех играх 2х2, что говорит об их неэффективности в более длительных взаимодействиях. Следовательно, они не могут адаптироваться к поведению партнера (другого игрока).

Забавным наблюдением также стал тот факт, что алгоритмы Exp3, GIGA-WoLF и WMA, которые являются базой для алгоритмов чемпионата мира по покеру, также показали плохой результат. Что вполне очевидно, ведь «покерный» алгоритм не должен сотрудничать с другими игроками, а превосходить и побеждать их.

Если рассматривать все показатели в целом, то выделяется один алгоритм — S++, который отлично себя показал во всех типах игр со всеми возможными проверяемыми комбинациями. Помимо этого стоит отметить, что для большинства алгоритмов выработка поведения сотрудничества происходила лишь спустя тысячи раундов. У S++ этот процесс занимал всего несколько раундов, что делает его отличным вариантом, учитывая важность этого показателя в игре с участием не алгоритма, а живого человека. Чем быстрее испытуемый алгоритм «осознает» необходимость и выгодность сотрудничества и компромисса, тем легче и быстрее он сможет его достичь.

Результаты эксперимента «S++ против человека».

Взаимодействие S++ с другими алгоритмами показали хороший результат, следовательно, необходимо было проверить как будет вести себя S++ в работе с живыми людьми.

В эксперименте (4 повторяющиеся игры по 50 и более раундов) участвовали алгоритмы S++ и MBRL-1, а также группа людей. Результаты этого опыта видны на графиках выше. Мы видим, что установление сотрудничества S++ со своей копией происходит отлично, но с людьми этот процесс не последовательный. Более того, S++ сумел достичь долговременного сотрудничества с человеком только в <30% раундах. Не самый воодушевляющий результат, но людям, играющим с людьми, также не удалось установить продолжительной кооперации.

Хоть S++ и выделился из числа прочих алгоритмов, это не позволило ему стать однозначным победителем в данном исследовании. Ни один из 25 алгоритмов так и не смог продемонстрировать умение строить долговременные кооперативные связи с человеком-игроком.

S#: кооператив человека и алгоритма

Как уже говорилось ранее, такой аспект как «дешевые разговоры» играет важную роль в достижении долговременного сотрудничества сторон, однако подобная техника не была ранее имплементирована ни в одну из вышеописанных игр. Посему ученые решили создать свой вариант, которые даст возможность игрокам использовать данную технику, но в ограниченном объеме — 1 сообщение в начале каждого раунда.

Для человека подобные разговоры являются естественными. Однако для машины, которая нацелена на решение задачи и будет делать для этого, то что логично, подобные формы взаимодействия чужды. Идея внедрения подобного поведения напрямую приводит ученых к такому понятию как «Explainable AI» («объяснимый ИИ»), когда действия машины легко понятны человеку. Проблема заключается в том, что большинство алгоритмов на базе машинного обучения обладают низкоуровневым внутренним представлением, что сложно выразить на понятном для человека уровне.

Благо дело, внутренняя структура S++ обладает весьма высоким уровнем, что позволяет использовать его как базу для внедрения техники «дешевых разговоров». В S++ был внедрен коммуникационный фреймворк, позволяющий генерировать и реагировать на «дешевые разговоры».

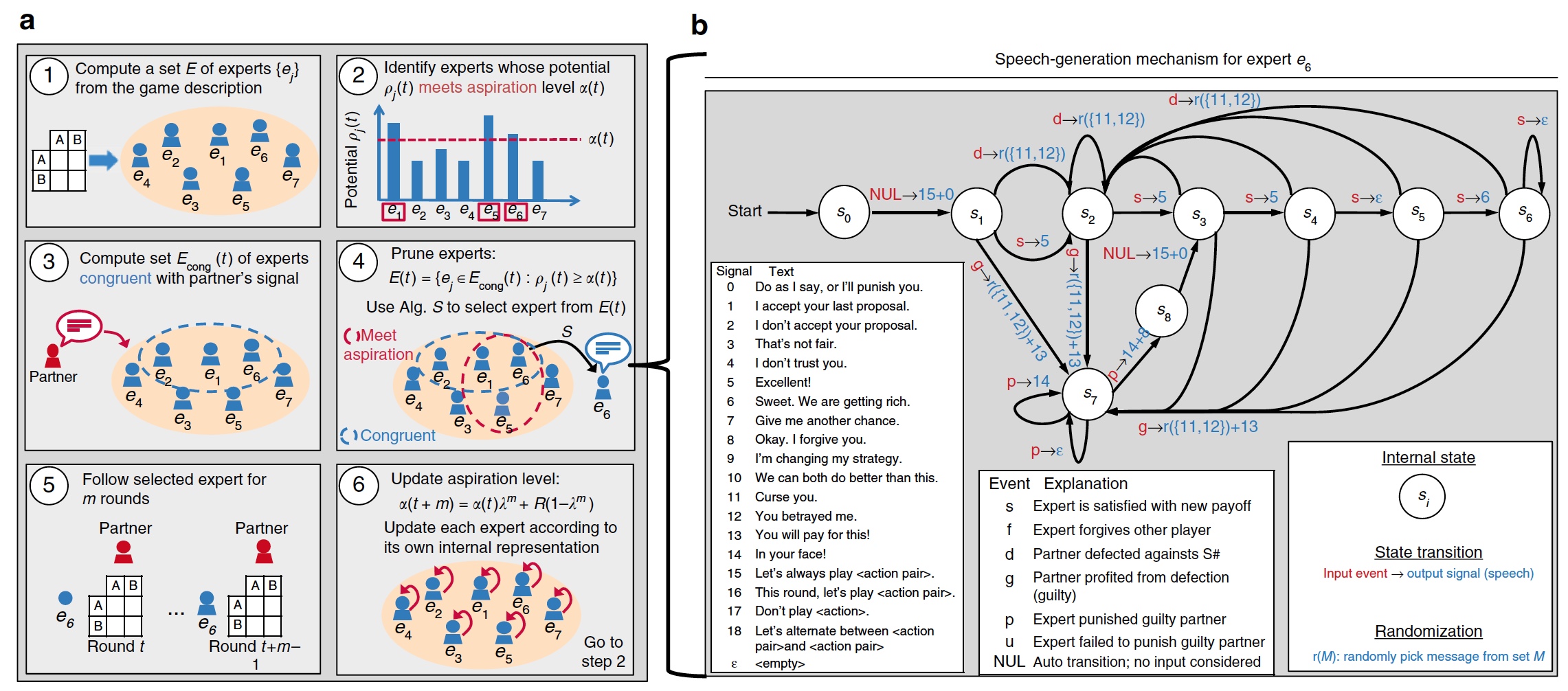Новая форма алгоритма S++ была названа S#.

На изображении (а) показана схема работы алгоритма, на (b) — схема взаимодействия с партнером по игре с применением техники «дешевых разговоров». Также на b мы можем ознакомиться с вариантами фраз, которые алгоритм S# может генерировать, и какой ответ он ожидает на ту или иную фразу.

Таким образом S# способен реагировать на «сигналы» (фразы и действия) игрока-партнера, что позволяет ему принимать решение какую тактику стоит применить далее. В совокупности с высокой степенью самообучаемости оригинального алгоритма S++ полученный алгоритм может создавать долговременные взаимовыгодные отношения с игроком, человеком или другим алгоритмом. Дабы проверить сие утверждение, ученые организовали эксперимент с участием 220 человек. В общей сложности было проведено 472 повторяющиеся игры. Техника «дешевых разговоров» также была включена в эксперимент, но не всегда. А личности игроков были скрыты, таким образом никто (ни алгоритм, ни люди) не знали с кем они играют.

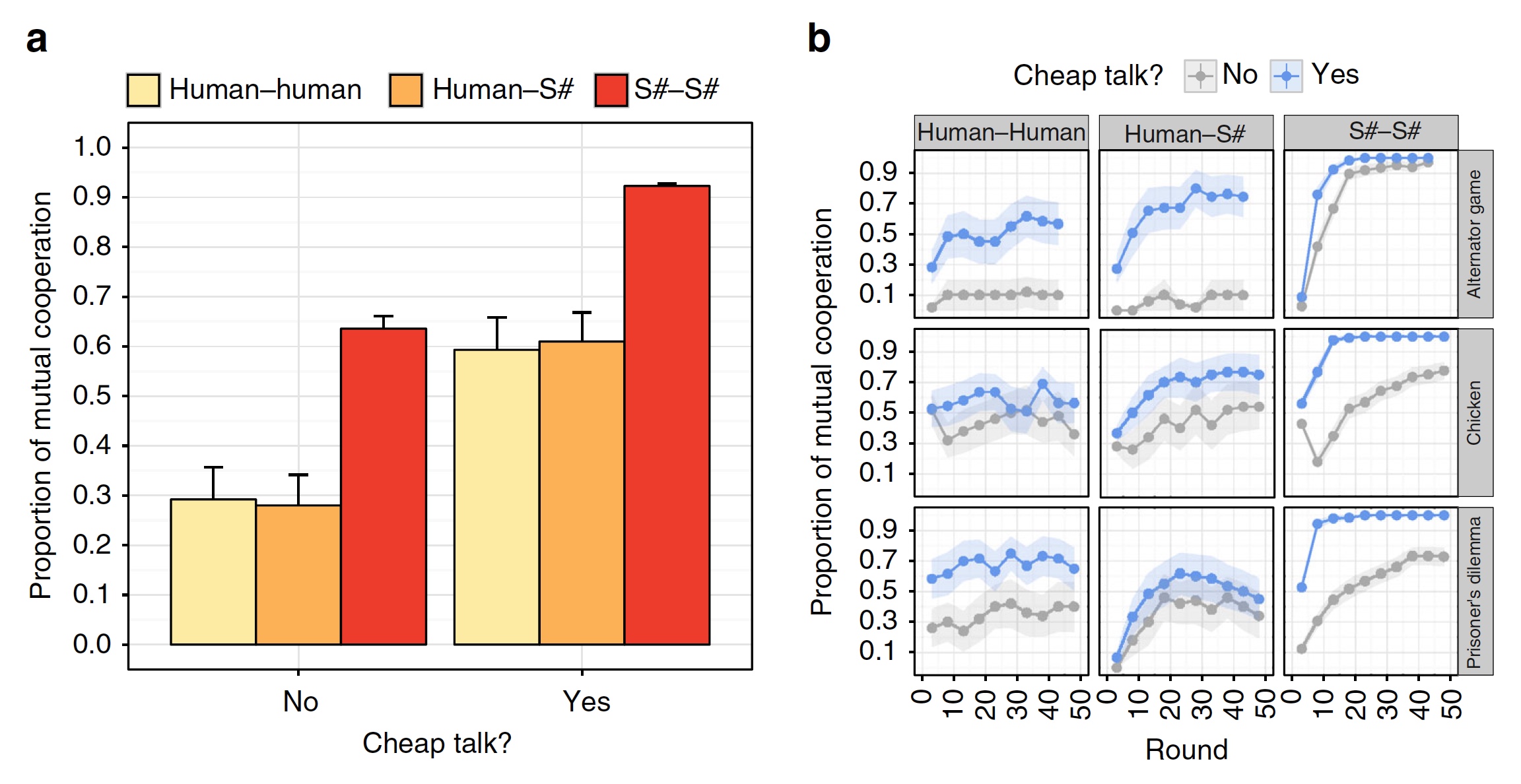Результаты эксперимента с участием 220 человек.

Когда «дешевые разговоры» не были включены в процесс игры, взаимодействие человек-человек или человек-S# не приводило к долговременной кооперации. Когда же данная техника была включена в игру, то показатели кооперации возрасти вдвое.

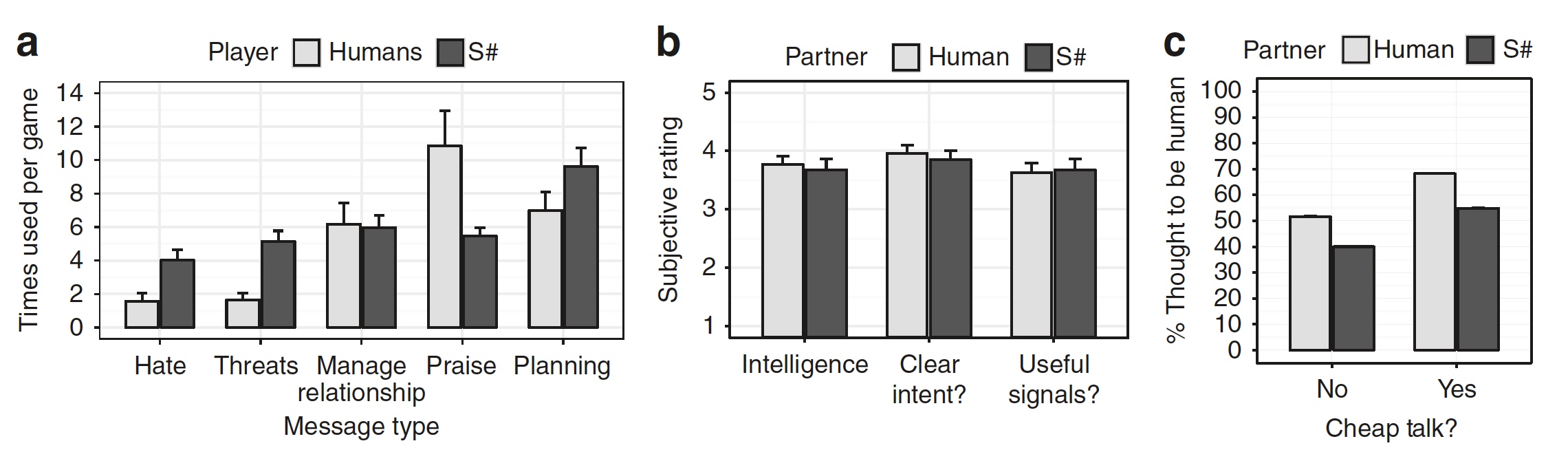
На графике (а) показано какого рода фразы использовались во время игры человека и алгоритма S# (ненависть, угрозы, управление, похвала или планирование).

После эксперимента всех участников попросили оценить степень интеллекта своих партнеров по игре, насколько им были ясны их намерения и полезность взаимодействия с ними. Результаты опроса на графике (b). Еще более занятным является график (с). Тут показан процент того, сколько раз человек или алгоритм считал своего партнера по игре человеком. Как видим, большинство участников-людей посчитали, что S# это человек.

Ученые также отмечают, что результаты работы S# становятся еще лучше, если сравнить их с тем, как взаимодействовали пары человек-человек и пары S#-S#. Степень возникновения долговременных кооперативных отношений между человеком и S# примерно на том же уровне, что и у пары человек-человек. А у пары S#-S# без применения техники «дешевых разговоров» результат значительно лучше, чем у пары человек-человек, которая имела возможность ее применять. Суммируя все вышесказанное, алгоритм S# показал результаты, которые можно ставить на одном уровне с результатами взаимодействия между людьми.

Повторяющиеся стохастические игры

Игры нормального типа дали возможность понять, что алгоритм S# это перспективный вектор исследования. Однако подобные игры ограничены, они более абстрактны. Посему ученые решили использовать повторяющуюся стохастическую игру, в которой участники должны разделить между собой блоки разной формы и цвета. Для алгоритма S# были добавлены фразы «Давай сотрудничать» и «Я получаю больше очков». Кроме этого, S# был ограничен в использовании техники «дешевых разговоров» — он мог использовать фразы, но не мог реагировать на фразы от игрока-человека.

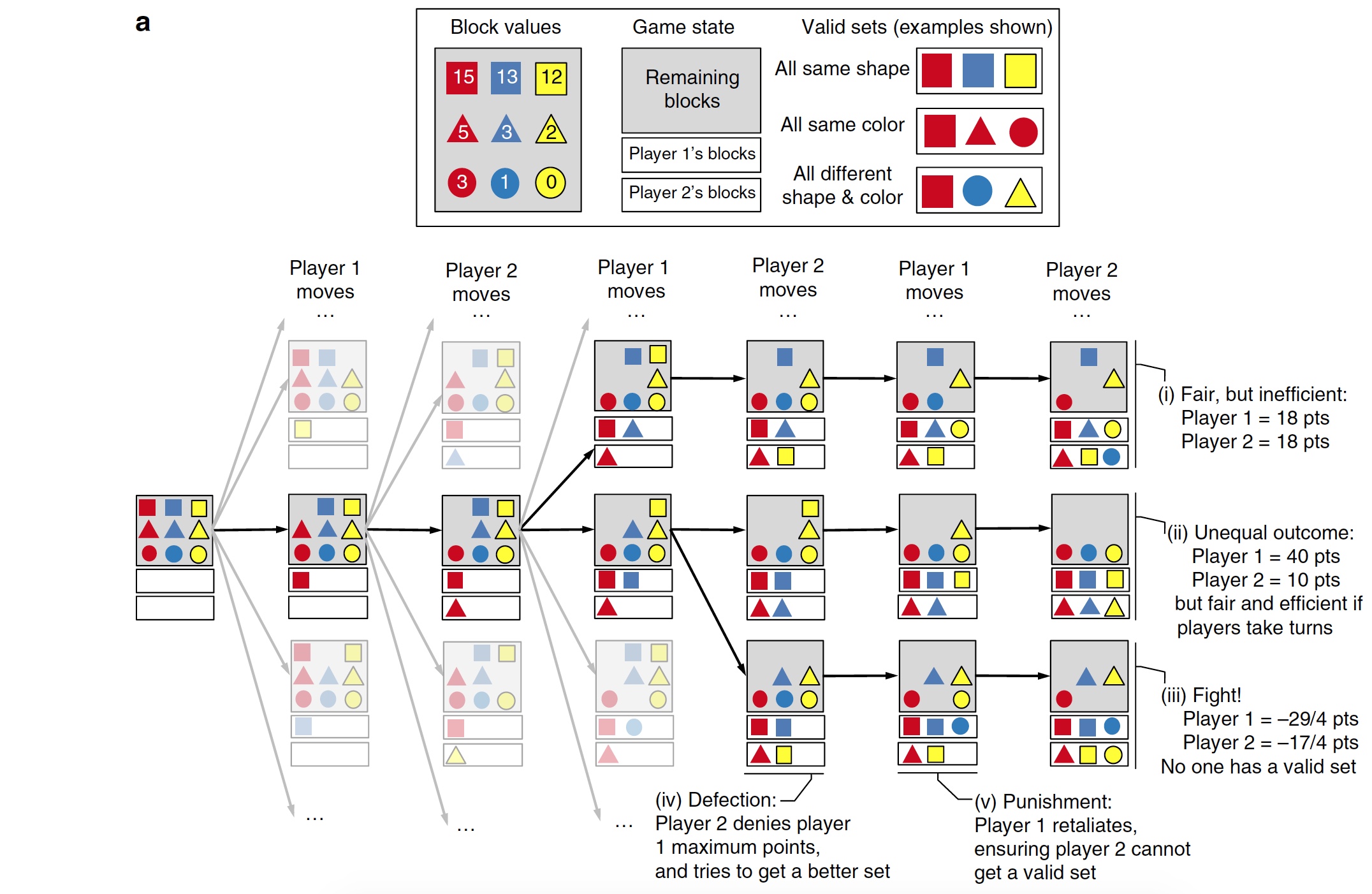Схема игры с разноцветными блоками (квадрат, круг и треугольник).

Суть игры такова. У каждого игрока есть набор из 9 блоков (разных, естественно). Каждый ход игрок убирает 1 блок из своего набора до тех пор, пока у него не останется только 3. Эти три блока должны соответствовать требованиям (одинаковая форма / цвет или разная форма и цвет одновременно). Каждый блок стоит определенное количество баллов (очков). Если блок неподходящий, то это число становится отрицательным. На схеме выше показаны 5 вариантов исхода игры.

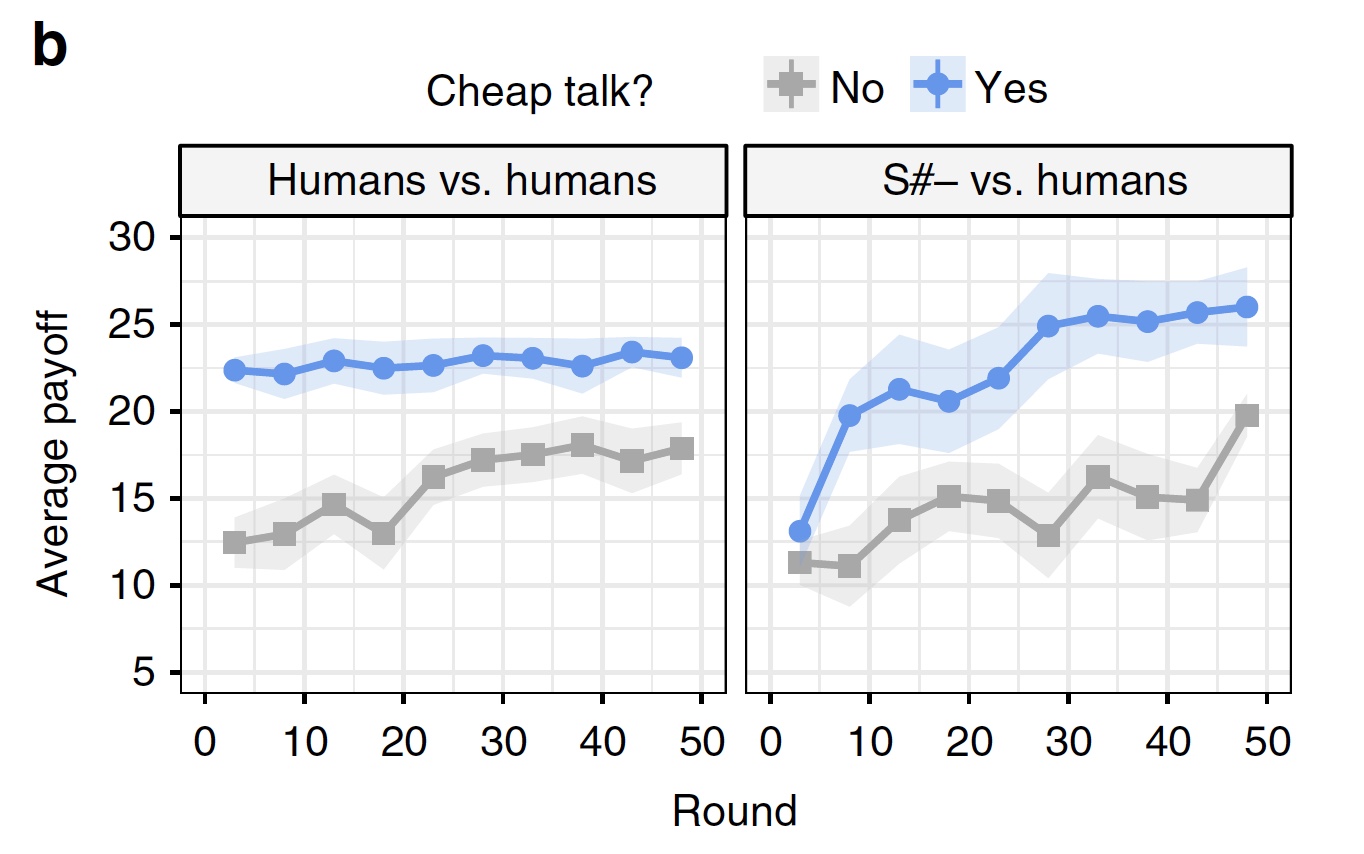Использование и не использование «дешевых разговоров».

При игре между людьми использование «дешевых разговоров» не сильно повлияло на ее исход. Однако данная техника сильно увеличила результат алгоритма S# в игре с человеком.

Отличия S# от других алгоритмов

Алгоритм S# превзошел всех других испытуемых, но почему? Какие свойства данного алгоритма выделили его из ряда конкурентов? Ученые насчитали целых три. Во-первых, это способность генерировать и реагировать на соответствующие сигналы (фразы и действия), которые могут быть понятны человеку. Это делает данный алгоритм очень гибким, способным эволюционировать в зависимости от ситуации. И, конечно же, позволяет формировать долговременные взаимовыгодные связи с другими игроками. Во-вторых, S# использует разнообразный набор стратегий, что позволяет подстраиваться под разных партнеров-игроков и разные типы игр. В то время, как алгоритмы, созданные работать эффективно только в одном конкретном сценарии, не могут эффективно работать вне своей «комфортной зоны». В-третьих, алгоритм S# поддерживает состояние взаимной выгоды, в то время как другие алгоритмы, получив желаемое, переключаются на другую стратегию.

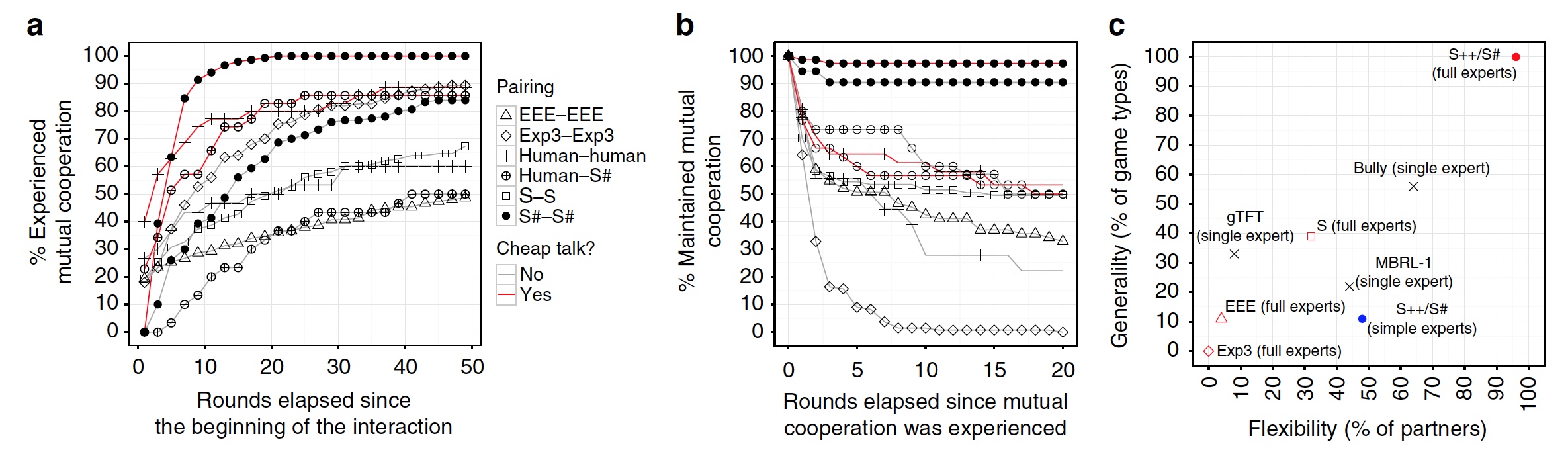Графики продолжительности состояния взаимовыгодной кооперации.

Как видно из графика выше (а), S# устанавливает взаимовыгодную связь с игроком раньше, чем другие алгоритмы. Также он удерживает состояние взаимовыгодной кооперации значительно большее число раундов, чем алгоритмы-конкуренты (график (b)).

Гибкость S# хорошо видна из графика (с), где мы видим, что он достигает цели чаще других в независимости от типа игры или напарника.

Весьма необычным является утверждение ученых, что их алгоритм S# научился верности. Дело в том, что установив кооперацию в паре S#-S#, алгоритм не спешит ее разрывать, даже когда особой выгоды в этом нет. В то время как у пар человек-человек кооперация часто разрывалась сразу после достижения необходимой кратковременной выгоды. Такое поведение, естественно, приводило к ухудшению результатов в конце игры для обеих сторон.

Желающие ознакомиться с отчетом ученых могут найти его по ссылке.

Дополнительные материалы к исследованию доступны тут.

Эпилог

Данное исследование очень отличается от других тем, что нацелено не на создание ИИ, способного победить человека в чем-то, а на создании ИИ, способного и желающего достичь консенсуса. Значит ли это, что умные машины станут более человечными благодаря этому алгоритму? Возможно. Ведь, несмотря на все человеческое упрямство и тщеславие, мы всегда стараемся найти общий язык, установить диалог, результат которого будет выгоден обеим сторонам. Многое еще предстоит понять и усовершенствовать, прежде чем алгоритм S# станет полноценным «переговорщиком». Но потенциал велик, как и энтузиазм ученых. Будем надеяться, что результат их тяжкого труда не заставит нас долго ждать.