Сотрудники Санкт-Петербургского политехнического университета Петра Великого (СПбПУ) предложили оригинальную теорию описания структуры квазикристаллов с икосаэдрической симметрией, приблизившись к решению одной из важнейших задач современного материаловедения — расшифровке структуры этих необычных веществ. Работа отечественных ученых попала на обложку ведущего научного журнала Лондонского королевского общества — Proceedings of the Royal Society A.

До недавнего времени строение квазикристаллов рассматривалось в рамках шестимерной кристаллографии, что сильно усложняло расчеты и не позволяло получить простую и наглядную картину. Однако в 2015 году, благодаря работам Алексея Мадисона из Политехнического университета появилась возможность решения данной проблемы в трехмерном пространстве. Он в течение многих лет занимается теорией квазикристаллического состояния — в частности, описанием и расшифровкой структуры икосаэдрических квазикристаллов.

«Все, как в обычных кристаллах, с единственными отличиями — имеется четыре типа элементарных ячеек вместо одной, а заполнение пространства идентичными копиями ячеек идет по принципу подобия, а не трансляции», — поясняет Мадисон.

Расположение атомов в структуре кристаллов определяется на основе анализа дифракционных картин. Уравнение дифракции для обычных кристаллов предложил Уильям Брэгг, который благодаря этой работе стал самым молодым Нобелевским лауреатом в истории. Сейчас хорошо известно, что если в кристалле на разности хода между двумя последовательными атомными плоскостями укладывается целое число длин волн, то рассеянные лучи придут в одной фазе, давая при определенных углах резкие дифракционные пики.

Что будет в ситуации, если расстояния между соседними плоскостями не равны друг другу, а чередуются, например, в соответствии с последовательностью Фибоначчи? Будут ли появляться брэгговские пики, или будет присутствовать только лишь диффузный фон? На этот вопрос в 1982 году ответил Дан Шехтман, поразив научное сообщество дифракционной картиной с симметрией пятого порядка. Это противоречило основному закону кристаллографии, согласно которому оси 5-го порядка несовместимы с периодической решеткой. После долгой борьбы с неприятием нового, в 2011 году Дан Шехтман был удостоен Нобелевской премии.

В квазикристаллах любой фрагмент структуры повторяется бесконечно много раз, повторяется строго закономерно, но не периодически. Определить разность хода между выбранной плоскостью и каждой последующей, а затем еще и усреднить соответствующие фазовые множители казалось просто невозможным. Однако Мадисон нашел неожиданное решение — он предложил построить специальную матрицу по аналогии с матрицей подстановок, и провел ее анализ.

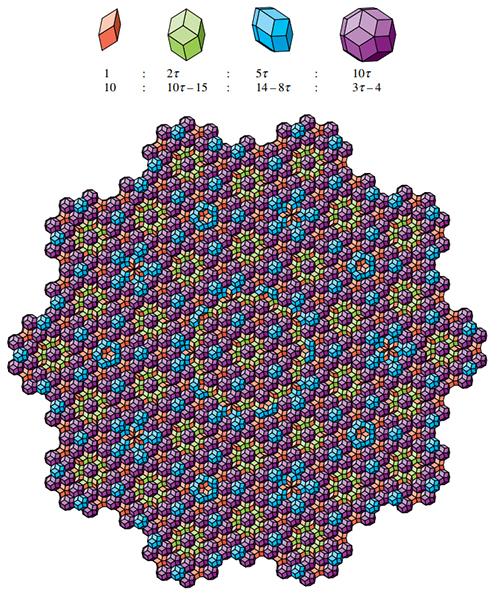Четыре типа элементарных ячеек (сверху) и схематическая структура икосаэдрических квазикристаллов (снизу) / СПбПУ

В итоге задача свелась к вычислению структурных факторов для каждого типа элементарных ячеек. Авторы продемонстрировали работоспособность метода, разбив квазикристалл с икосаэдрической симметрией на четыре типа ячеек.