На первый взгляд существует принципиальная разница между прозрачными объектами и непрозрачными, пусть даже и не поглощающими свет, такими как снег, бумага или биологическая ткань. Последние, благодаря многократному рассеянию света в них, могут создать непроницаемую завесу для наблюдателя.

Информация о первоначальном волновом фронте, падающем на такую поверхность от предмета, кажется безвозвратно утраченной. Однако когерентность света не теряется даже после тысячи актов рассеяния, так что теоретически изображение может быть восстановлено. Сделать это можно с помощью методов матричной оптики, для которой кубик сахара-рафинада является такой же оптической системой, как и линза, различаясь только количеством элементов: если первая описывается матрицей передачи 2х2, то количество строк и столбцов в матрице второй исчисляется сотнями тысяч и миллионами. Конечно, такой огромный массив информации обработать крайне сложно, поэтому методы матричной оптики оказываются практически бесполезными в экспериментах с рассеивающими средами, и более разумным подходом является использование усредненных характеристик, полученных путем измерения интенсивностей, пусть даже и с потерей информации о фазе.

Однако прогресс информационных технологий в перспективе может сделать задачу полного восстановления информации вполне реальной. Демонстрацией принципиальной возможности такого восстановления стала работа сотрудников Института Ланжевена в Париже, в которой 70 микронный слой цинковых белил (ZnO) превращался в линзу, фокусирующую свет, или в прозрачный объект, сквозь который можно было видеть изображение (рис. 1а). На первом этапе исследователи путем сравнения опорного пучка и света, рассеянного на слое белил, получали матрицу передачи из 256х256 элементов.

Затем, используя информацию о матрице, они с помощью пространственного модулятора света (жидкокристаллический экран 16х16 пикселей) видоизменяли фронт падающей волны таким образом, чтобы в результате прохождения сквозь слой цинковых белил свет фокусировался в точку на некотором расстоянии от преграды, превращая, таким образом, рассеивающий объект в прозрачную линзу. Разумеется, изменив соответствующим образом распределение напряжений на жидкокристаллическом экране, можно создать такие фазовые задержки, что луч сфокусируются в несколько точек или в другую фигуру. Нетрудно сообразить, что в силу обратимости хода лучей точки фокуса могут выступать в качестве источников света, которые остаются видимыми даже за рассеивающим экраном (рис. 1б).

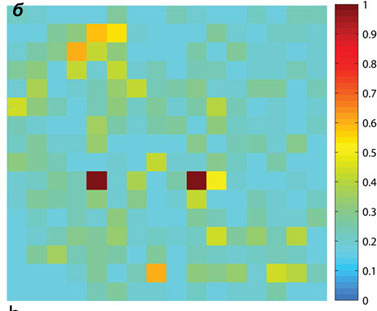Рис. 1. а – Линза в матричной оптике представляется матрицей передачи 2х2 (f – фокусное расстояние линзы), в то время как кусочек сахара-рафинада характеризуется матрицей с гораздо большим числом элементов. Если матрица передачи рассеивающего объекта известна, его можно тоже превратить в линзу [2]. б – Результат наблюдения двух светящихся точек сквозь слой цинковых белил (цветная шкала показывает интенсивность света) [1]

Конечно, в данном случае речь идет о совсем небольшом экране – с площадью порядка нескольких квадратных микрон. Вообще же для участка рассеивающей поверхности площадью S, освещаемой длиной волны l, соответствующая матрица передачи будет включать NґN элементов, где N определяется по формуле N = 2πS/l2. В случае площадки размером 1 мм² N составит уже миллионы – многовато даже для новейших компьютеров, так что любители занавесок из тюля могут еще долго оставаться спокойными.

Применение подходов матричной оптики может, тем не менее, существенно обогатить методы оптической микроскопии, например, позволит смотреть сквозь слои рассеивающей свет среды и следить за процессами в клетках живых биологических тканей, а не только в специально приготовленных препаратах и срезах.

1. S.M.Popoff et al., Phys. Rev. Lett. 104, 100601 (2010).
2. E.G. van Putten, A.P.Mosk, Physics 3, 22 (2010).