Автор: man_of_letters. Если одной метафорой, то произошли первые испытания термоядерной бомбы. Специалисты с благоговейным ужасом и радостью смотрят на поднимающийся над планетою гриб. Остальное человечество живёт обычной жизнью, пока не зная, современниками какого события они являются. Мне нравилось изучение цифровых технологий, сильнее интересовала только работа человеческой психики и междисциплинарное знание, которое можно объединить под условным названием «общая теория информации». Эти увлечения позволили увидеть в смене цифр смену эпох. Постараюсь объяснить суть случившегося максимально доступно.

GPT-4 технически считается языковой моделью. Языковая модель — это программа, которую проще всего представлять как систему исправления опечаток на стероидах.

Допустим, вы набираете кому-то сообщение: Сегдн, ткй чдунсный день!

Программа исправляет ошибки и предлагает возможное продолжение: Сегодня такой чудесный день! Я отлично выспался, а так как сегодня выходной, то я смогу увидеться со своими друзьями и замечательно проведу время.

Или это что-то вроде книжки «1000 смешных шуток». Пользователь выбирает тему, находит нужный раздел и тыкает пальцем наугад. Это в самом грубом приближении.

В действительности книг не одна, а сотни тысяч. Фрагмент выбирается не один, а тысячи. А далее происходит поиск образцов текста в тех же книжках, чтобы использовать их в качестве шаблона для составления структуры текста. Подходящие с какой-то вероятностью слова будут подставлены в наиболее подходящий текст. Таким образом машина получает результат, который из-за элемента случайности иногда выходит нормальным. Чем больше языковая модель, тем больше у неё образцов текста, т.е. выше её шансы собрать удачный коллаж из слов.

Подобные программы оперируют космосом из обрывков предложений, им дела нет до смысла и содержания текстов. Каким-то «знанием» на этом уровне можно считать запоминание правильных склонений и расстановку запятых, правда, это достигается не за счёт выявления свода правил языка, а как механический результат большой «начитанности».

И так было до GPT-4.

CEO OpenAI делится историей разработки

Когда создание текста машиной стало демонстрировать первые адекватные результаты, в тему стали вливать деньги. Деньги — это возможность запихнуть в модель больше текста. А больше текста — это лучшее качество результатов. Но одновременно обучение сверхбольших моделей стало демонстрировать нелинейные эффекты. Например, модели научились считать. То, есть подозрительно часто угадывать результаты простых арифметических действий. Какое то время большинство скептиков придерживалось теории, что модель не считает, а просто цитирует по памяти учебники. Правда оказалась интересной.

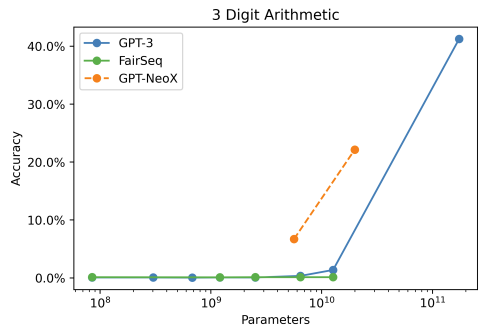Точность арифметических действий с ростом модели

График показывает, что начиная с некоторого размера модели, у неё резко открывается математический талант. Изучение вопроса показало, что в текстах, использованных для обучения не присутствует достаточного количества примеров для зубрёжки ответов. Модель усвоила то, как из цифр, связанных знаками математических операций, следует производить новые цифры, но не разобралась в десятичной системе счисления, поэтому точность не 100%. Эксперименты демонстрируют, что можно показать ChatGPT выдуманную систему записи чисел, и модель будет решать задачки в этой системе с точностью выше случайной.

Очень важно правильно понять этот факт. В системе, предназначенной для связывания букв, начиная с некоторого объёма изученных данных, самоорганизуется специализированная логика, пытающаяся считать числа. В нейросети изначально никакой логики нет, есть коробка с логическими элементами, которые она соединяет в процессе обучения. Кажется, что логические элементы языковой модели должны жонглировать только буквами. Как может алгоритм делать что то непредусмотренное создателями? Будем разбираться.

Языковая модель – это граф

Граф — это математическая штука, представим лабиринт с множеством дверей, имеющий один вход и один выход. На входе стоит хранитель лабиринта, которому вы сообщаете свой вопрос, в ответ он выдаёт первый ключ с числом. Вы находите дверь с этим числом, открываете дверь, берёте второй ключ за дверью и повторяете это долго долго, открывая новые двери, пока не попадёте в зал «всех ответов«. Там стоит машина, похожая на однорукого бандита, только барабанов у неё не три, а несколько сотен, на каждом из них есть все буквы алфавита. Остаётся вставить собранные ключи в эту машину, и барабаны повернутся, показав ответ на вопрос.

Эта машина не знает ничего, числа на ключах сами по себе не значат ничего, только лабиринт знает ответы. Ответ — это путь от двери к двери, знание зашифровано в последовательности коридоров.

Ну граф и граф, не герцог же, зачем в таком странном виде хранить знание о множестве вещей? Почему бы не использовать понятные базы данных? Тут принцип простой: если информацию нельзя уложить в табличку Excel, то и базу использовать не выйдет. Знание, выраженное естественным языком, не имеет единообразной структуры, нужна долгая ручная работа, чтобы разложить содержание текста на смысловые фрагменты. Такое делается для решения профессиональных задач, но это не универсальный подход.

Существуют разные способы обработки неструктурированных данных, но действительно выстрелил способ шинковки текста на маленькие кусочки. В этих обрывках алгоритмы ищут взаимосвязи. Взаимосвязи машины производят в виде гигантских таблиц с числами, в которых каждое число является стеной, дверью или коридором лабиринта. Важны не только сами числа, алгоритмы предписывают схему связи между этими числами. В свою очередь граф — это стандартный способ описания связей между объектами. Так и получается, что языковая модель — это граф.

Количество связей в графе быстро растёт

При добавлении новых коридоров в лабиринт, количество разных способов дойти до конца растёт c чудовищно ускоряющимся темпом. В языке есть несколько десятков букв, но с их помощью можно составить сотни тысяч слов. Графы — это эффективный способ хранить взаимосвязи между текстовыми элементами. Если попробовать визуализировать разные пути прохождения сигнала в небольшой языковой модели, то получится космическая лапша.

Связи между тысячами элементов

МРТ мозга рыбы во время всплеска активности

Этот рыб тут нужен не только для кросоты. Хотя работа биологических информационных систем совсем не похожа на алгоритмы машинного обучения, но концептуально это такое же множество связей между группами элементов. И это была первая причина, почему стоит относиться к языковым моделям серьёзно.

Понимают ли модели предыдущего поколения смысл текстов? Нет. Но как тогда они создают новую информацию? Что хранится в графе? Что вообще они делают? Давайте на минутку включим фантазию и представим, что где то живёт художник, который придумал себе нишу в совриске. Начинает он рабочий процесс с того, что доверившись потоку, малюет нехитрую мазню цветными кремами для тортов. Затем берёт матрицу из губок и прикладывает к новому творению. На матрице остаётся грубая копия оригинала. Взяв лист бумаги, творец делает оттиск. Получается нечто, напоминающее оригинал, но какое то скучное. На творца снисходит вдохновение и, переставляя губки местами, он делает 10 работ, которые чем то напоминают исходное изображение, но являются новыми произведениями.

Губки впитали в себя некоторую информации о разных фрагментах картины. Поэтому с помощью этих губок можно создать подобие исходной картины, или нечто иное, а можно скомбинировать с губками, содержащими следы других картин. Эти действия можно доверить роботу, который по случайному алгоритму будет переставлять губки. При этом часть таких творений будет сложно отличить от работ самого художника.

Элементы графа — это губки, которые впитывают фрагменты информации. Связи в графе организованы иерархически: нижняя часть содержит типичные сочетания губок, а верхняя часть — сочетания сочетаний.

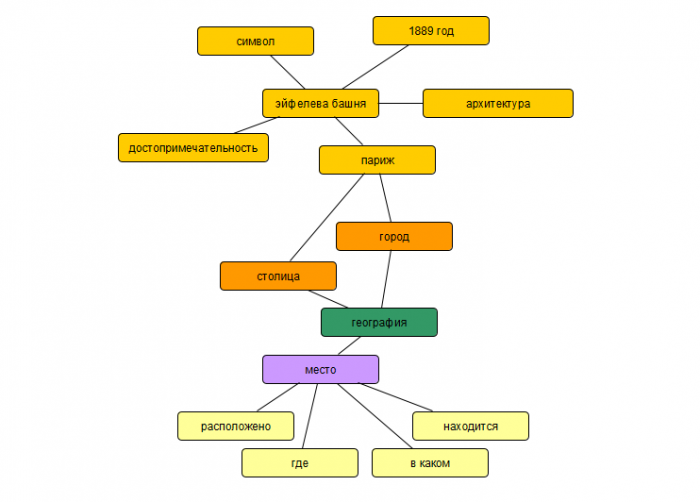Нижний уровень графа

Так выглядит нижний уровень языковой модели. Просто связи между словами. Но этой маленькой структуры достаточно, чтобы модель ответила на такие вопросы: Где находится Эйфелева башня? Какие есть в Париже архитектурные достопримечательности? В каком году был построен символ Парижа?

Банальная статистика, но алгоритм уже может находить ответы на вопросы, выраженные произвольно на обычном языке. Такая система работает подобно механическим часам, все связи наблюдаемы, никакой магии.

Длительный процесс вычисления взаимосвязей ласково именуют «обучением». Скорее это дрессировка железной палкой. Представьте, что вам предлагают сыграть в компьютерную игру, на экране появляется поле квадратиков, случайно заполненное коридорами, стенками, дверями разных цветов. Ваш герой появляется в одному углу, выход в другом. В начале раунда вам показывают последовательность из нескольких цветов. Чтобы выход открылся, вам необходимо пройти через двери в указанном порядке цветов. Вы можете свободно перемещать двери и коридоры по полю. Вы выстраиваете путь к выходу, проходите через двери в правильной цветовой последовательности и выход открывается. Начинается следующий раунд: появляется новая комбинация цветов, вы прокладываете следующий путь рядом и выходите. Так повторяется 1000 раз. Игра переходит в режим начисления очков: вам демонстрируется 100 комбинаций цветов, и если вы пройдёте через соответствующие двери до выхода, то получите очко. Тут до вас доходит, что если создавать не разные пути, а максимально хитро переиспользовать уже расставленные двери и коридоры, это даст больше баллов. При этом те комбинации, которые были использованы на первом этапе, во время подсчета очков вам уже не покажут, потому что вообще то вы должны искать закономерности в сочетании цветов. Потому что задача нейросети состоит не в умении найти выход по известной схеме, а выйти из лабиринта для максимального количества новых схем.

Нейросеть раз за разом пробегает через гигабайты данных, если алгоритм попытается зубрить информацию, злые учёные заметят это и сломают зубрилку. Зубрить — значит выстраивать коридоры, повторяя схемы, вместо поиска закономерностей. В таких тяжелых условиях алгоритм потихоньку запоминает случайные инсайты, которые помогают угадывать большее количество правильных ответов.

Эта была не слезливая история про угнетение роботов, это объяснение того, почему нейросеть учится в состоянии стресса и главная её цель — это оптимальное расходование ресурсов. Это имеет интересное следствие. Пока модель небольшая, ей дела нет до вычисления математических примеров, если её не обучают этому намеренно, потому что ей надо уметь нормально обрабатывать тексты.

Когда модели становятся большими, тексты уже неплохо обрабатываются и есть свободная память, алгоритм начинает «замечать», что решение математических примеров повышает баллы в тестах. Встаёт выбор: либо сохранить как можно больше вариантов арифметических операций с ответами, либо придумать что то хитрое и не тратить ресурсы зря. Например, запоминание сумм трёхзначных чисел условно потребует 2 001 000 связей, при этом ответы будут на 100% правильные. С другой стороны можно сохранить только 210 связей для операций с однозначными числами и применять их для решения всех примеров подряд, часто совершая ошибки. 222+444 = 666 верно! 16+25=31 неверно, перенос десятки не сделан!

И тут нейросеть смекает, что за ошибки в математике её не бьют, а за ошибки в текстах бьют больно, и полезнее потратить 2 миллиона связей на что то другое. Ну, конечно, так написано для красоты, просто из всех связей остаются только те связи, которые приносят максимум баллов. Так в нейросети появляется примитивный движок математической логики. Встретили цифры и арифметические операции? В калькулятор!

Простите, лень рисовать все линии

Тут целых две прелести: функционально происходит счёт, а не манипуляции с текстом, а ещё где то перед калькулятором принимается решение, что кусок текста является арифметическим примером. Языковая модель научилась новой функции, потому что это было экономичным решением! И эта подсистема более универсальна, чем текстовая модель, потому что не содержит все варианты решения в явном виде, это уже знание счета в нашем обычном понимании. То, что компьютер может считать, это не удивительно, то, что компьютер использовал закономерность, которую его не просили искать — это восхитительно.

Описанное поведение верно для версии GPT-3. В техническом отчёте, посвященном четверке, разработчики пишут, что уже намеренно учили систему математике. Речь идёт о задачках начальной школы, сформулированных в текстовом виде. Например: у Пети было 100 яблок, 30% он отдал Маше и т. д. Это задачи на математическую логику и простейшие арифметические действия. Система решила 8500 задач с точностью 92%.

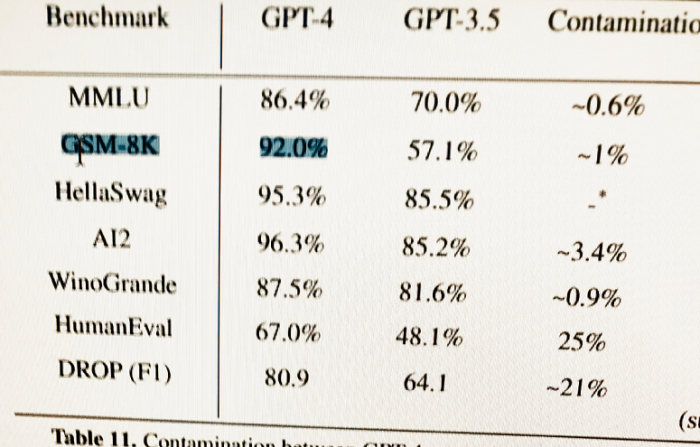
Л – значит логика

Дальше только больше.